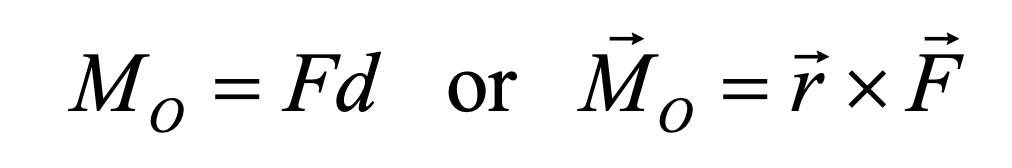Cuerpos Rígidos
Un cuerpo rígido es un cuerpo ideal en el que sus partículas tienen posiciones relativas fijas entre sí.
Estos cuerpos no sufren deformaciones debido a la acción fuerzas externas. Se trata de cuerpos ideales ya que en la realidad los cuerpos no son completamente rígidos sino que se deforman por la acción de fuerzas externas.
A diferencia de las partículas, en los cuerpos rígidos sí consideramos sus dimensiones además de su masa.
En la unidad estática del cuerpo rígido se estudian las condiciones necesarias y suficientes para que un cuerpo rígido permanezca en equilibrio.
Estos cuerpos no sufren deformaciones debido a la acción fuerzas externas. Se trata de cuerpos ideales ya que en la realidad los cuerpos no son completamente rígidos sino que se deforman por la acción de fuerzas externas.
A diferencia de las partículas, en los cuerpos rígidos sí consideramos sus dimensiones además de su masa.
En la unidad estática del cuerpo rígido se estudian las condiciones necesarias y suficientes para que un cuerpo rígido permanezca en equilibrio.
Sistemas de fuerza a estudiar:
1. Coplanar, sistema de fuerza paralela
2. Sistemas de fuerza coplanares, no paralelos, no concurrentes
3. Sistemas de fuerzas paralelas no coplanares
4. Sistemas de fuerza no coplanares, no paralelos, no concurrentes
1. Coplanar, sistema de fuerza paralela
2. Sistemas de fuerza coplanares, no paralelos, no concurrentes
3. Sistemas de fuerzas paralelas no coplanares
4. Sistemas de fuerza no coplanares, no paralelos, no concurrentes
Un sólido rígido es cualquier cuerpo formado por varios puntos materiales cuyas distancias mutuas permanecen constantes, incluso bajo la acción de fuerzas exteriores. En el cual las Fuerzas Originan Una Serie de Momentos.
Se dice que un cuerpo (rígido) está en equilibrio si la suma vectorial de TODAS las fuerzas y todos sus momentos tomados sobre cualquier punto es cero.
Principio de Transmisibilidad.
Una fuerza aplicada sobre un cuerpo rígido puede ser reemplazada por cualquier otra fuerza que tenga la misma intensidad y el mismo sentido y la misma dirección que la fuerza original y que se aplique sobre cualquier punto de su línea de acción.
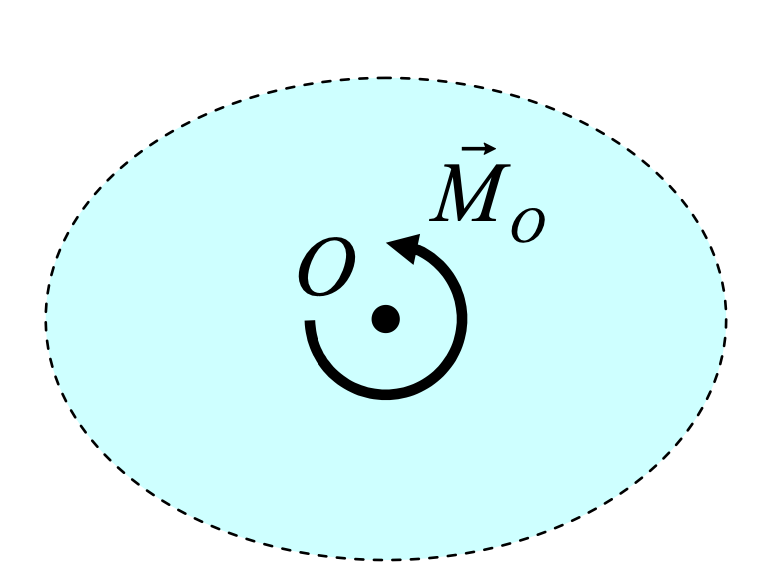
Momento de una fuerza.
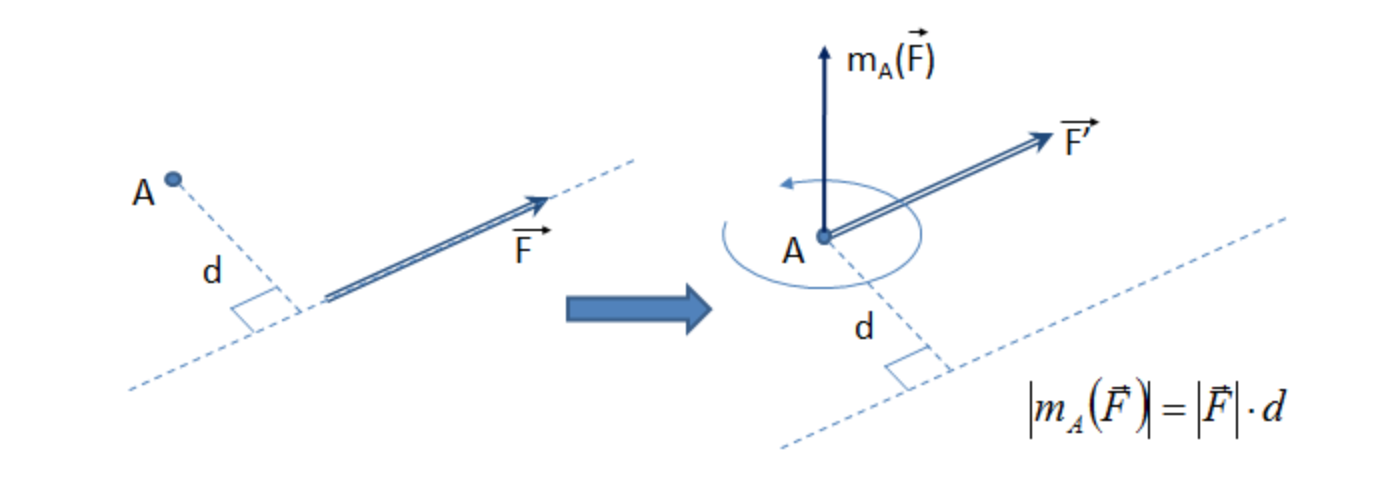
El momento de una fuerza se calcula cómo el producto vectorial entre la fuerza aplicada y el vector.
Sin embargo en muchas ocasiones el punto de aplicación de la fuerza no coincide con el punto de aplicación en el cuerpo. En este caso la fuerza actúa sobre el objeto y su estructura a cierta distancia, mediante un elemento que traslada esa acción de esta fuerza hasta el objeto.
Distancia que va desde el punto para el cual calculamos el momento (eje por el cual el cuerpo giraría) hasta el punto en dónde se aplica la fuerza. También recibe el nombre de torque.
El momento de una fuerza se calcula cómo el producto vectorial entre la fuerza aplicada y el vector.
Sin embargo en muchas ocasiones el punto de aplicación de la fuerza no coincide con el punto de aplicación en el cuerpo. En este caso la fuerza actúa sobre el objeto y su estructura a cierta distancia, mediante un elemento que traslada esa acción de esta fuerza hasta el objeto.
Distancia que va desde el punto para el cual calculamos el momento (eje por el cual el cuerpo giraría) hasta el punto en dónde se aplica la fuerza. También recibe el nombre de torque.
Un sólido rígido realiza un movimiento de rotación cuando sus partículas describen circunferencias alrededor de una recta llamada eje de rotación. Para caracterizar el estado de rotación de un cuerpo recurrimos en Física a su momento angular. Sabemos que para cambiar el momento angular, es decir, el estado de rotación del cuerpo, es necesario que actúe una fuerza que genere un momento respecto a un punto o eje de rotación.
En este apartado vamos a estudiar con cierto detalle dicho momento de fuerza. Además presentaremos un nuevo concepto: el par de fuerzas, que nos permitirá producir en los cuerpos un movimiento de rotación pura (esto es, sin traslación).
En este apartado vamos a estudiar con cierto detalle dicho momento de fuerza. Además presentaremos un nuevo concepto: el par de fuerzas, que nos permitirá producir en los cuerpos un movimiento de rotación pura (esto es, sin traslación).
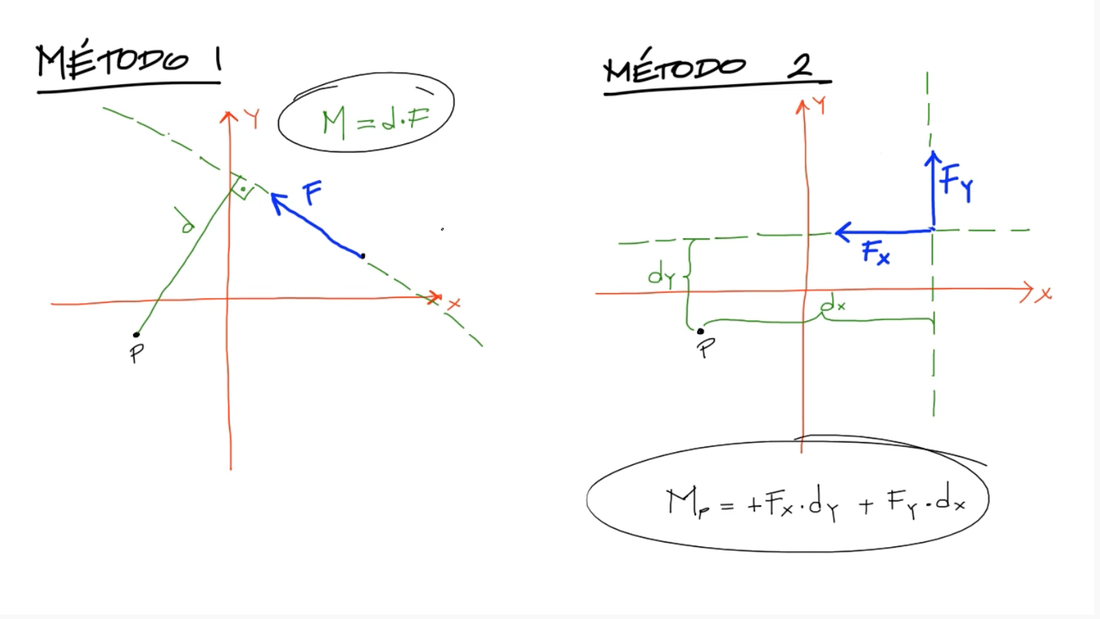
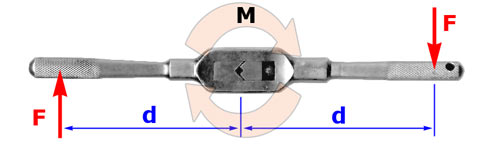
Momento de la Fuerza F, sobre la line A-A
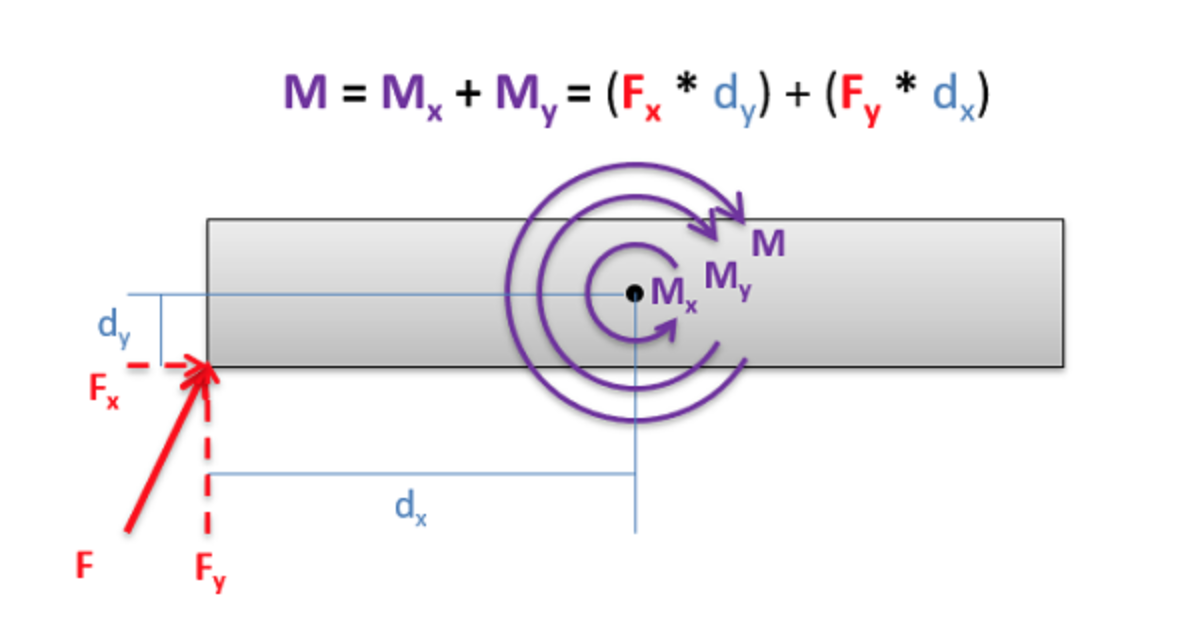
Cuando se usan cantidades escalares, la magnitud del momento será igual a la distancia perpendicular entre la línea de acción de la fuerza y el punto sobre el que estamos tomando el momento.
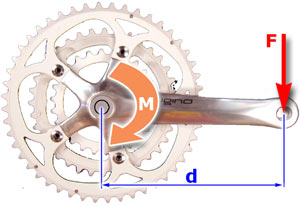
M = F X d
M = F X d
Ejemplo 1:
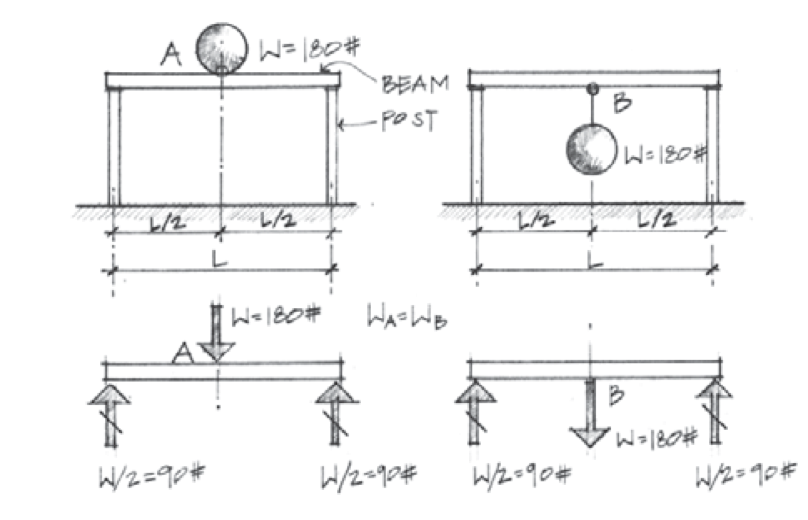
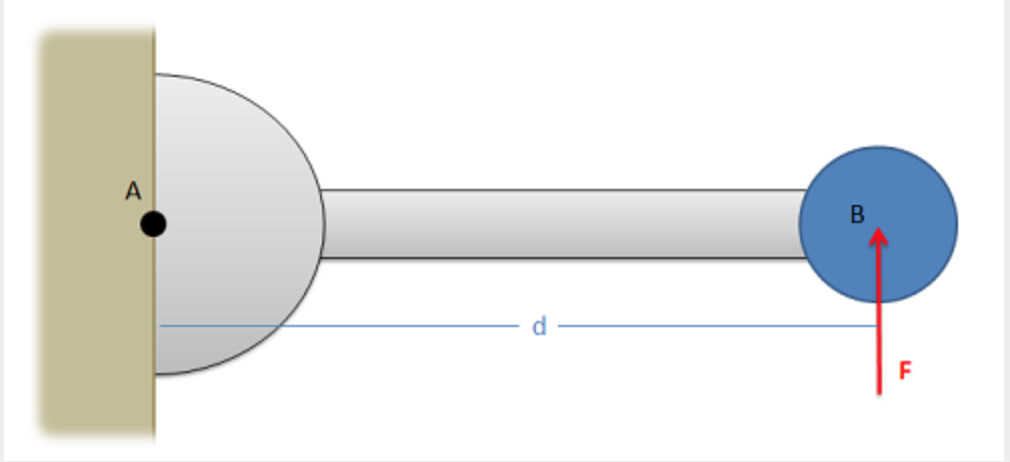
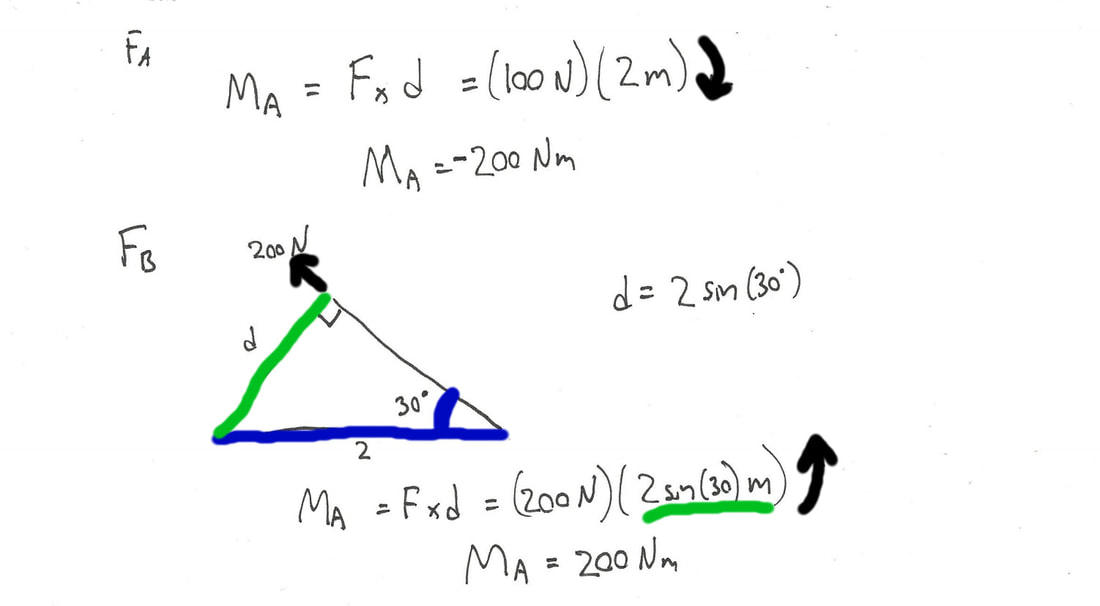
¿Cuál es el momento que ejerce la Fuerza A sobre el punto A?
¿Cuál es el momento que ejerce la Fuerza B sobre el Punto A?
¿Cuál es el momento que ejerce la Fuerza A sobre el punto A?
¿Cuál es el momento que ejerce la Fuerza B sobre el Punto A?
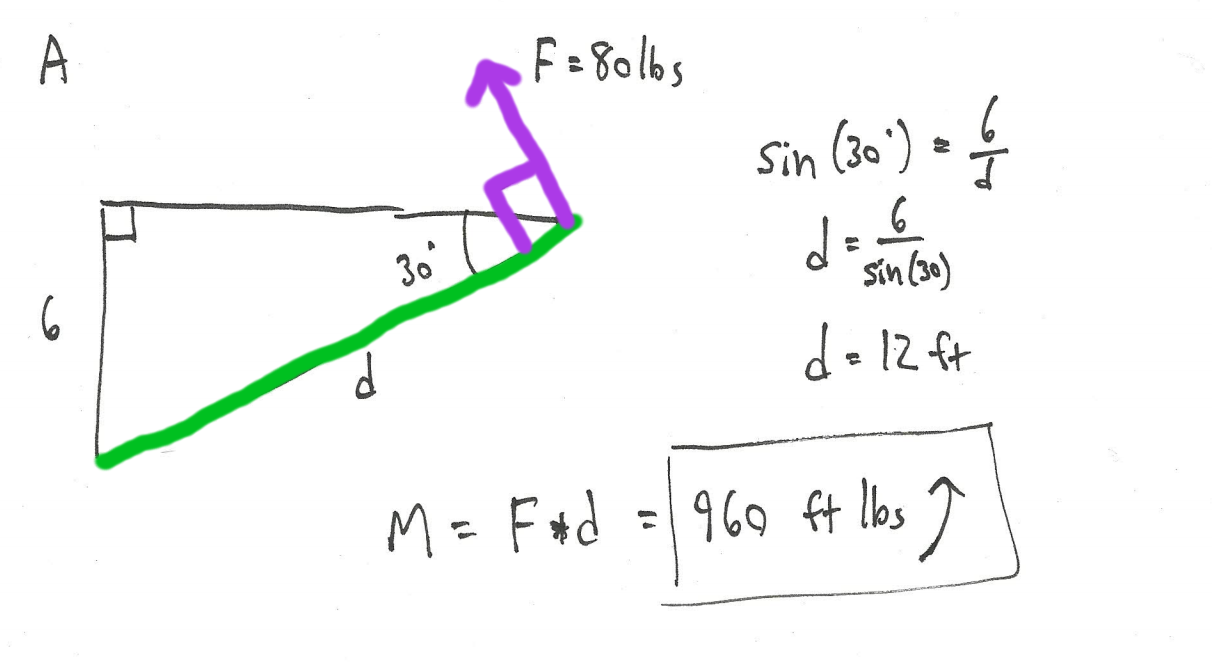
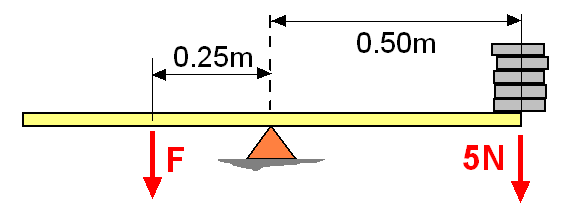
Ejemplo 2:
¿Cuál es el momento que ejerce esta fuerza sobre el punto A?
¿Cuál es el momento que ejerce esta fuerza sobre el punto B?
¿Cuál es el momento que ejerce esta fuerza sobre el punto A?
¿Cuál es el momento que ejerce esta fuerza sobre el punto B?
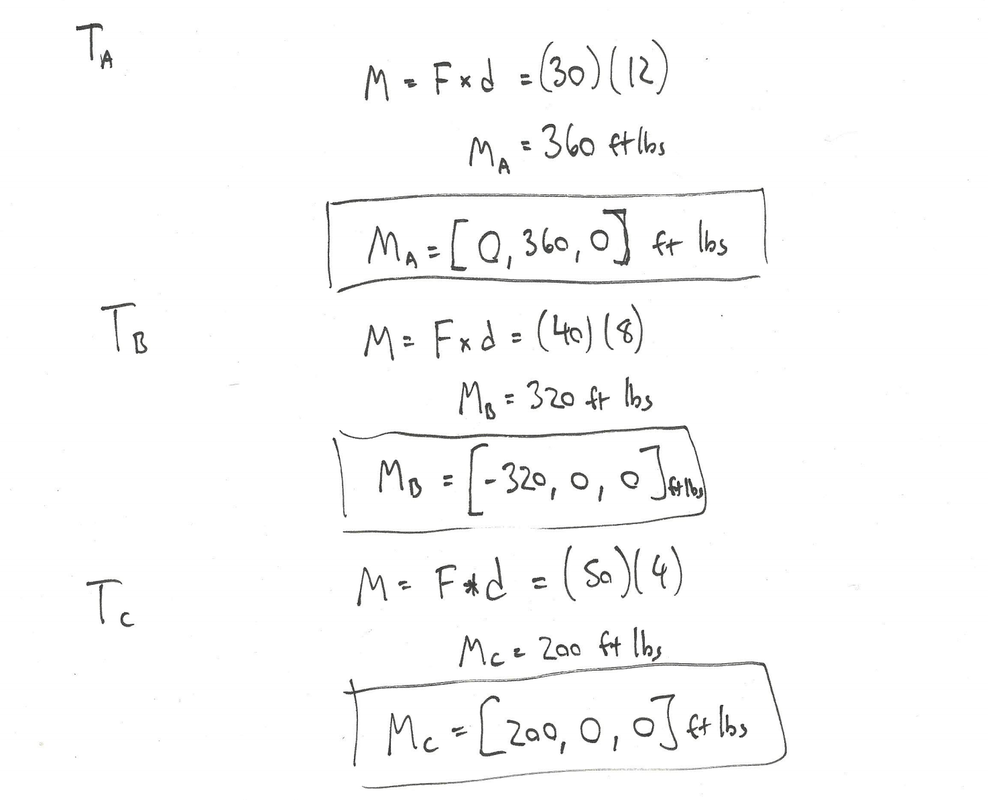
Ejemplo 3:
¿Cuáles son los momentos que ejercen cada una de las tres fuerzas de tensión sobre el punto A (el punto donde se juntan las vigas)?
¿Cuáles son los momentos que ejercen cada una de las tres fuerzas de tensión sobre el punto A (el punto donde se juntan las vigas)?
Teorema de Varignon
El teorema de Varignon , también llamado a menudo el principio de los momentos , es una herramienta muy útil en los cálculos de momentos escalares. En los casos en que la distancia perpendicular es difícil de determinar, el teorema de Varignon ofrece una alternativa para encontrar esa distancia
El teorema de Varignon , también llamado a menudo el principio de los momentos , es una herramienta muy útil en los cálculos de momentos escalares. En los casos en que la distancia perpendicular es difícil de determinar, el teorema de Varignon ofrece una alternativa para encontrar esa distancia
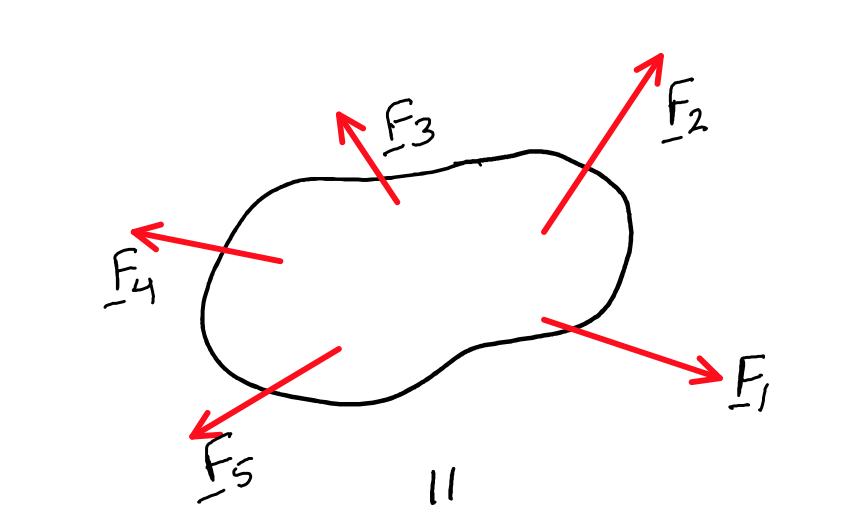
En su forma básica, Varignon afirma que si tenemos dos o más fuerzas concurrentes , la suma de los momentos que crea cada fuerza sobre un solo punto será igual al momento creado por la suma de esas fuerzas sobre el mismo punto.
Momento de una Fuerza Producto Vectorial
Ejemplo:
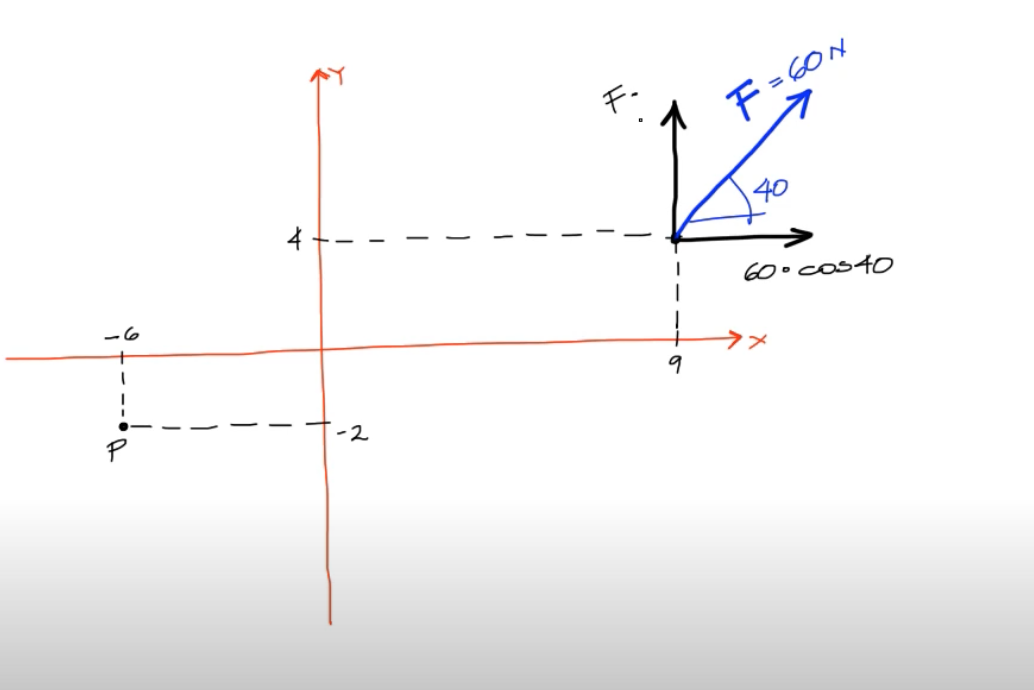
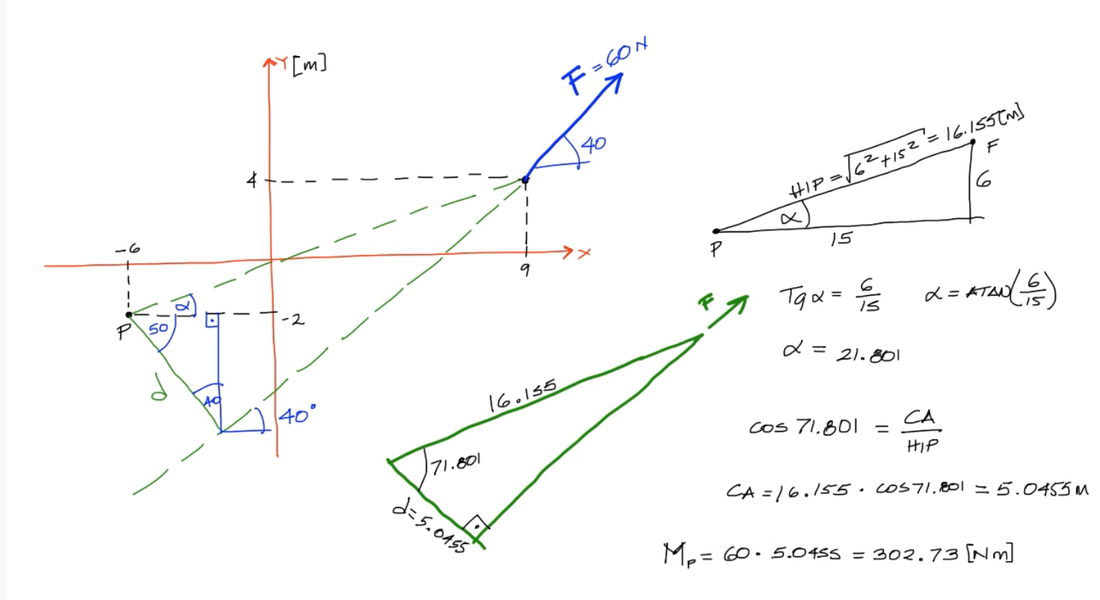
Encuentre el Momento producto de la Fuerza de 60 N, con respecto al punto indicado (p)
Encuentre el Momento producto de la Fuerza de 60 N, con respecto al punto indicado (p)
- a) Resuelva aplicando la definición de momento
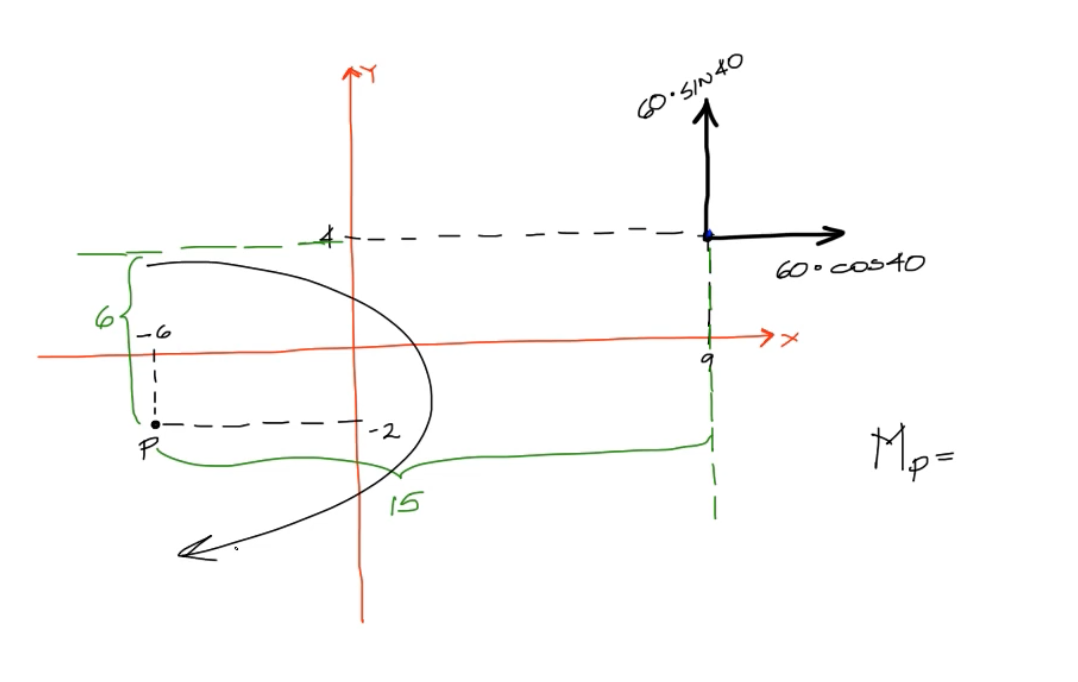
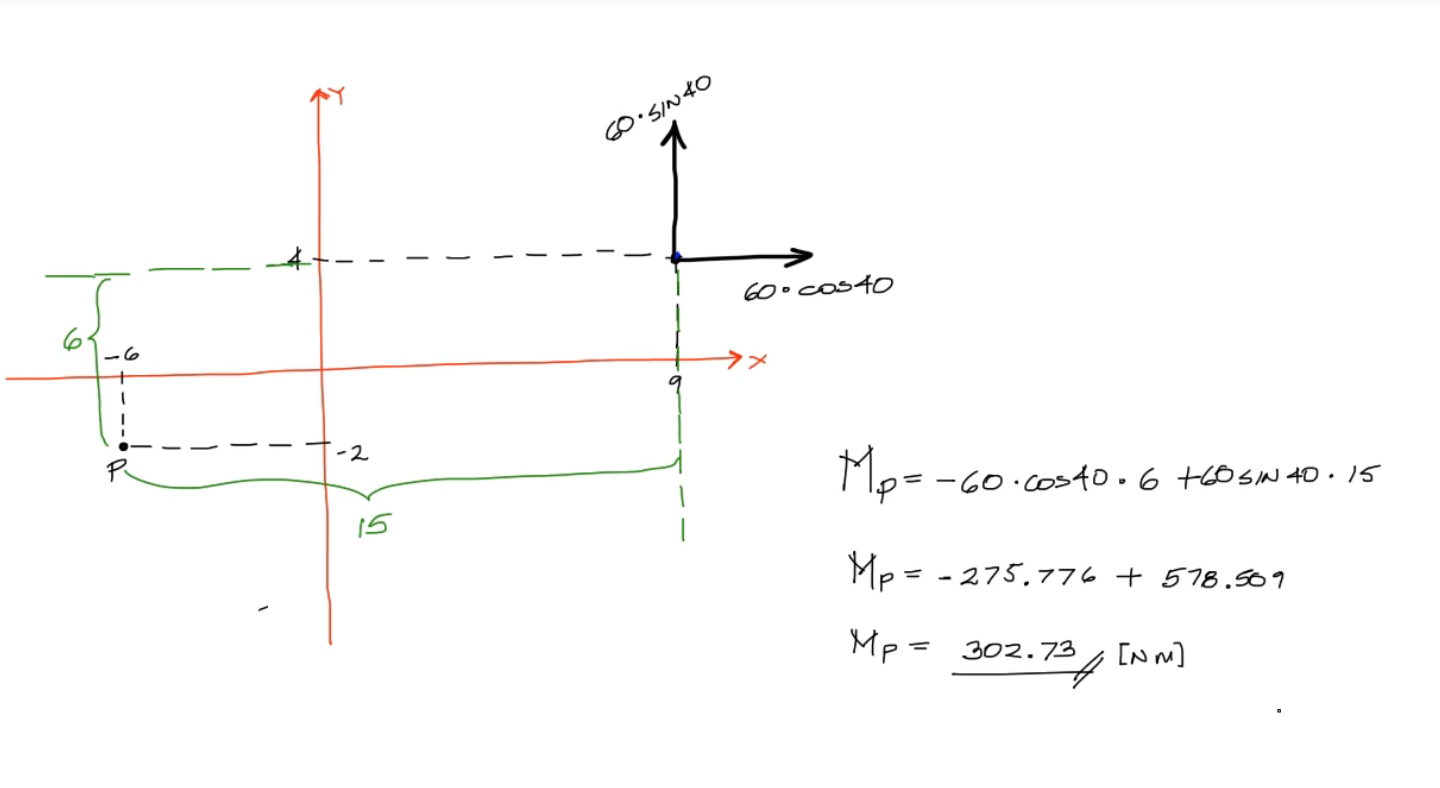
- b) Utilizando el Teorema de Varignon
- c) Producto vectorial.
Resolución a)
Resolución b)
Resolución c)
algo...
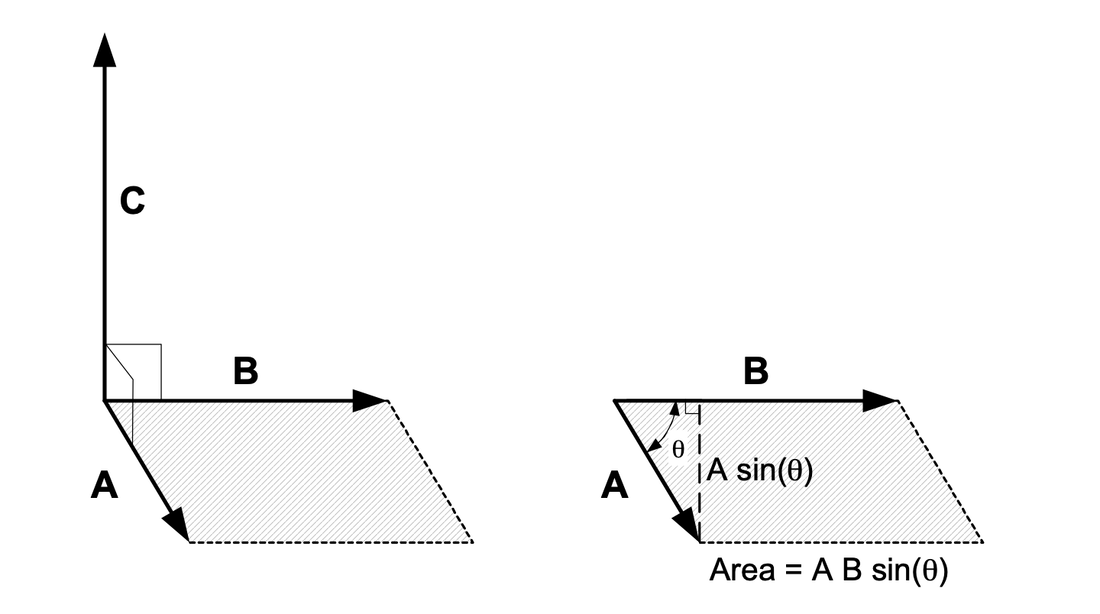
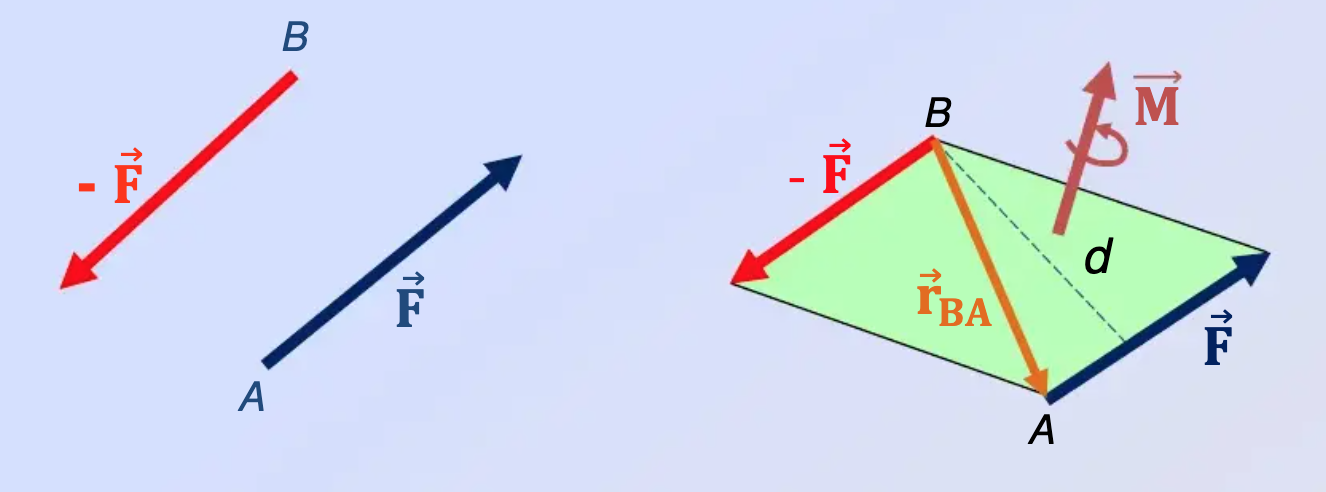
En términos geométricos, el producto cruzado de dos vectores, A y B, produce un nuevo vector, C, con una dirección perpendicular al plano formado por A y B (según la regla de la mano derecha) y una magnitud igual al área de el paralelogramo formado usando A y B como lados adyacentes.
Par de Fuerzas.
Una par de fuerza es un conjunto de fuerzas iguales y opuestas que ejercen un momento neto sobre un objeto pero no una fuerza neta. Debido a que la par de fuerzas ejerce un momento neto sin ejercer una fuerza neta, al par de fuerza también se les llama momentos puros
En muchas situaciones de equilibrio, una de las fuerzas que actúan sobre el cuerpo es su peso. En los diagramas de cuerpo libre, el vector de peso está unido al centro de gravedad del cuerpo. Para todos los propósitos prácticos, el centro de gravedad es idéntico al centro de masa, como aprendiste en Momento lineal y colisiones en momento lineal y colisiones.
Solo en situaciones en las que un cuerpo tiene una gran extensión espacial para que el campo gravitacional no sea uniforme en todo su volumen, el centro de gravedad y el centro de masa se encuentran en diferentes puntos.
Por lo tanto, a lo largo de este capítulo, usamos el centro de masa (CM) como el punto donde se une el vector de peso. Recuerde que el CM tiene un significado físico especial: cuando se aplica una fuerza externa a un cuerpo exactamente en su CM, el cuerpo en su conjunto experimenta un movimiento de traslación y dicha fuerza no causa rotación.
Solo en situaciones en las que un cuerpo tiene una gran extensión espacial para que el campo gravitacional no sea uniforme en todo su volumen, el centro de gravedad y el centro de masa se encuentran en diferentes puntos.
Por lo tanto, a lo largo de este capítulo, usamos el centro de masa (CM) como el punto donde se une el vector de peso. Recuerde que el CM tiene un significado físico especial: cuando se aplica una fuerza externa a un cuerpo exactamente en su CM, el cuerpo en su conjunto experimenta un movimiento de traslación y dicha fuerza no causa rotación.
Cuando el CM se encuentra fuera del eje de rotación, se produce un par gravitacional neto en un objeto. El par gravitacional es el par causado por el peso.
Este par gravitacional puede rotar el objeto si no hay soporte presente para equilibrarlo. La magnitud del par gravitacional depende de qué tan lejos del pivote se encuentre el CM.
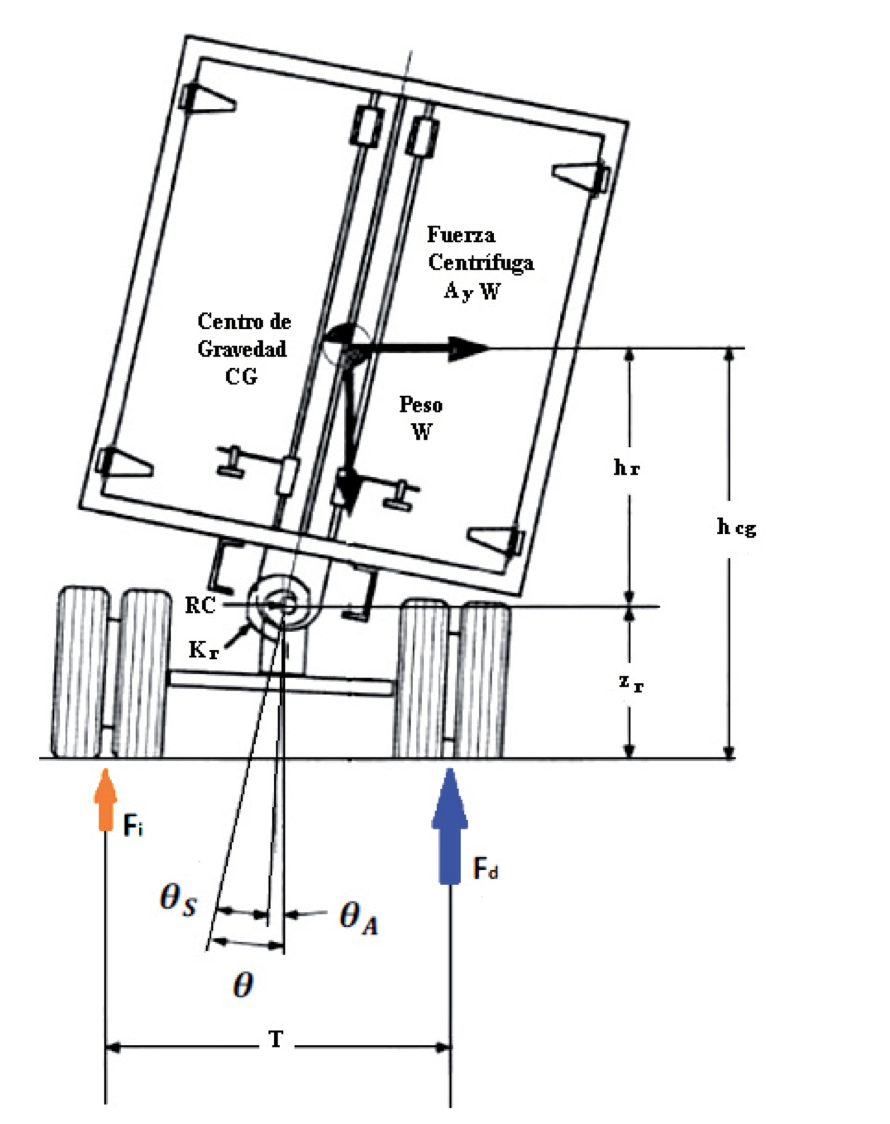
Por ejemplo, en el caso de un camión de carga (figura 2), el pivote se encuentra en la línea donde los neumáticos hacen contacto con la superficie de la carretera. Si el CM se encuentra muy por encima de la superficie de la carretera, el par gravitacional puede ser lo suficientemente grande como para volcar el camión.
Los automóviles de pasajeros con un CM bajo, cerca del pavimento, son más resistentes a vuelcos que los camiones.
Este par gravitacional puede rotar el objeto si no hay soporte presente para equilibrarlo. La magnitud del par gravitacional depende de qué tan lejos del pivote se encuentre el CM.
Por ejemplo, en el caso de un camión de carga (figura 2), el pivote se encuentra en la línea donde los neumáticos hacen contacto con la superficie de la carretera. Si el CM se encuentra muy por encima de la superficie de la carretera, el par gravitacional puede ser lo suficientemente grande como para volcar el camión.
Los automóviles de pasajeros con un CM bajo, cerca del pavimento, son más resistentes a vuelcos que los camiones.
En el siguiente simulador podrás experimentar la relación entre la altura del centro de gravedad y el ángulo de inclinación del plano.
Modifica estos factores y ve el resultando dando click sobre el boton de [Test]
Modifica estos factores y ve el resultando dando click sobre el boton de [Test]
Ejemplos:
Descomposición en una Fuerza y un Par
Dos fuerzas forman un par:
Si tienen la misma magnitud, líneas de acción paralelas y sentidos opuestos, como se muestra en la figura.
Si tienen la misma magnitud, líneas de acción paralelas y sentidos opuestos, como se muestra en la figura.
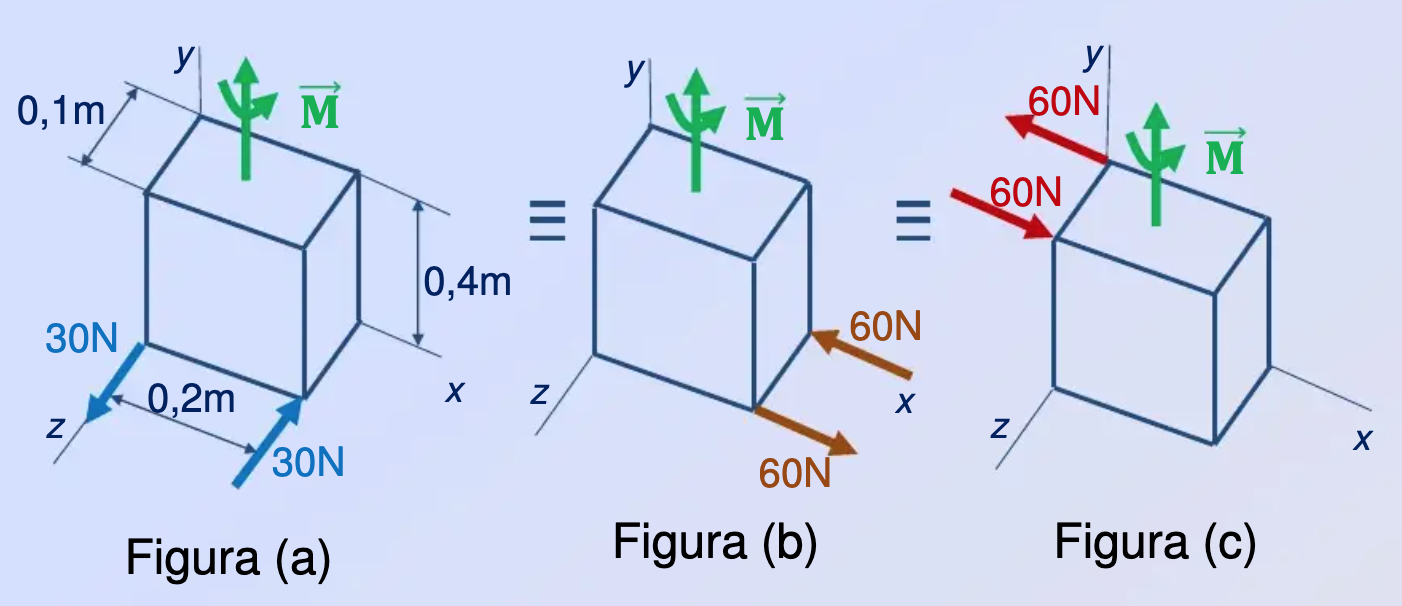
Pares Equivalentes:
Dos ó mas pares serán equivalentes si tienen el mismo momento, la misma dirección y la misma magnitud.
Dos ó mas pares serán equivalentes si tienen el mismo momento, la misma dirección y la misma magnitud.
Las figuras (b) y (c) muestran pares equivalentes aplicados sucesivamente sobre dicho paralelepípedo
Equilibrio de un cuerpo Rígido.
Un cuerpo rígido está en equilibrio si la suma de todas las fuerzas que actúan sobre él da una fuerza resultante = 0
- Suma de Fuerzas en X, Y, Z y
- Suma de Momento en un punto = 0
Ejemplo:
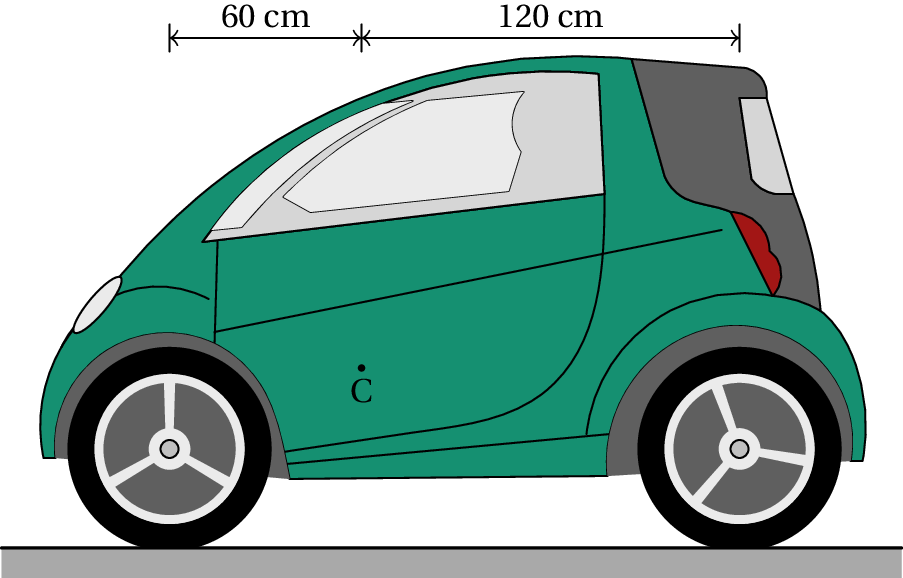
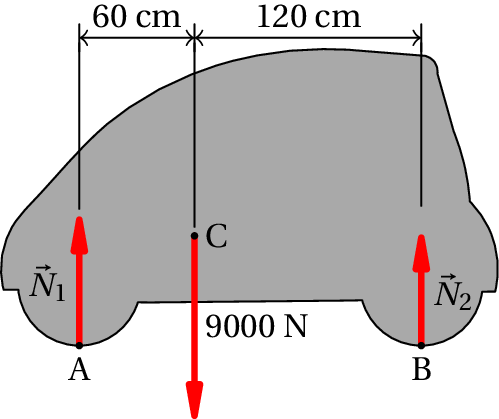
El automóvil de la figura se detiene en una carretera horizontal. El automóvil pesa 9000 N y su centro de gravedad, C, está 60 cm detrás del eje de las ruedas delanteras y 120 cm delante del eje de las ruedas traseras.
Encuentre la fuerza normal en cada neumático.
El automóvil de la figura se detiene en una carretera horizontal. El automóvil pesa 9000 N y su centro de gravedad, C, está 60 cm detrás del eje de las ruedas delanteras y 120 cm delante del eje de las ruedas traseras.
Encuentre la fuerza normal en cada neumático.
Resolución.
El automóvil está en equilibrio, ya que está en reposo. La figura de la derecha muestra el diagrama de cuerpo libre para el automóvil; N1 es la suma de las dos fuerzas normales en los neumáticos delanteros y N2 es la suma de las fuerzas normales en los neumáticos traseros.
La condición para que la suma de las fuerzas verticales sea cero es:
N1 + N2 = 9000 N
El automóvil está en equilibrio, ya que está en reposo. La figura de la derecha muestra el diagrama de cuerpo libre para el automóvil; N1 es la suma de las dos fuerzas normales en los neumáticos delanteros y N2 es la suma de las fuerzas normales en los neumáticos traseros.
La condición para que la suma de las fuerzas verticales sea cero es:
N1 + N2 = 9000 N
- Para encontrar el valor de estas dos variables, también debemos usar la condición de que la suma de los momentos de todas las fuerzas, sobre cualquier punto elegido, debe ser cero. La suma de los momentos sobre el punto A es:
- 1.8 N2 − 0.6×9000=0 ⇒N2=3000N
- Ahora hacemos suma de momento en el punto B
- 1.2×9000 − 1.8 x N1=0 ⇒N1=6000N
Sistema Equivalente.
Apoyos y Reacciones.
Calculo de Reacciones.
Objetivos de aprendizaje
Al final de este capítulo, debería poder:
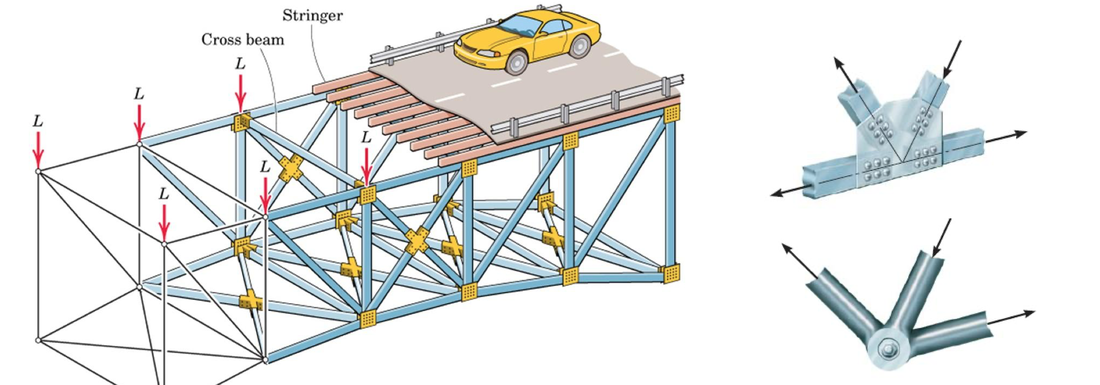
Conocer elementos estructurales longitudinales (VIgas)
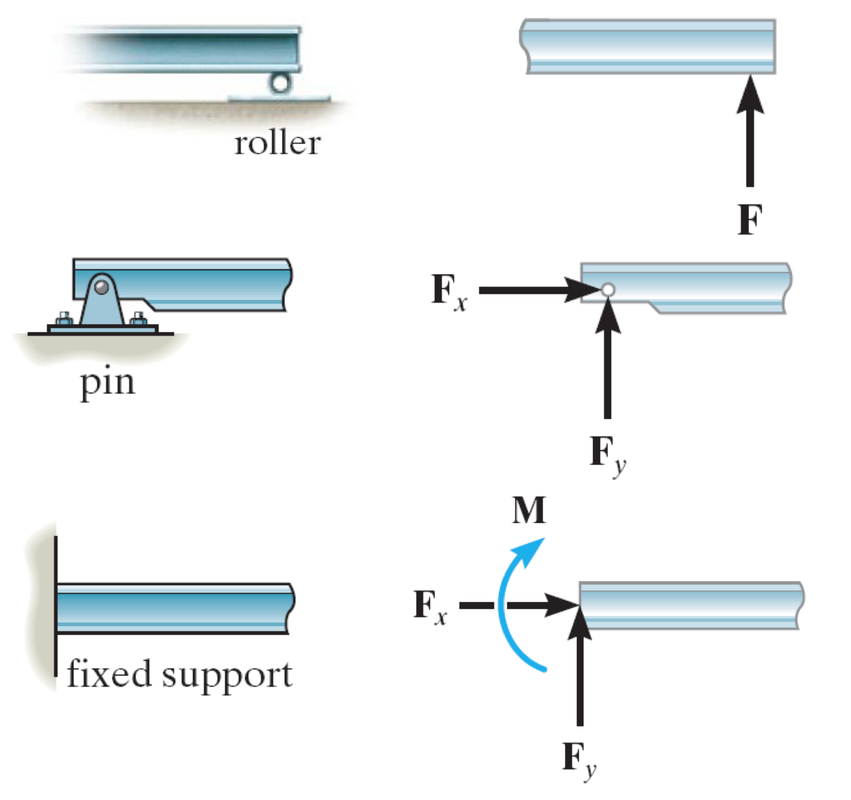
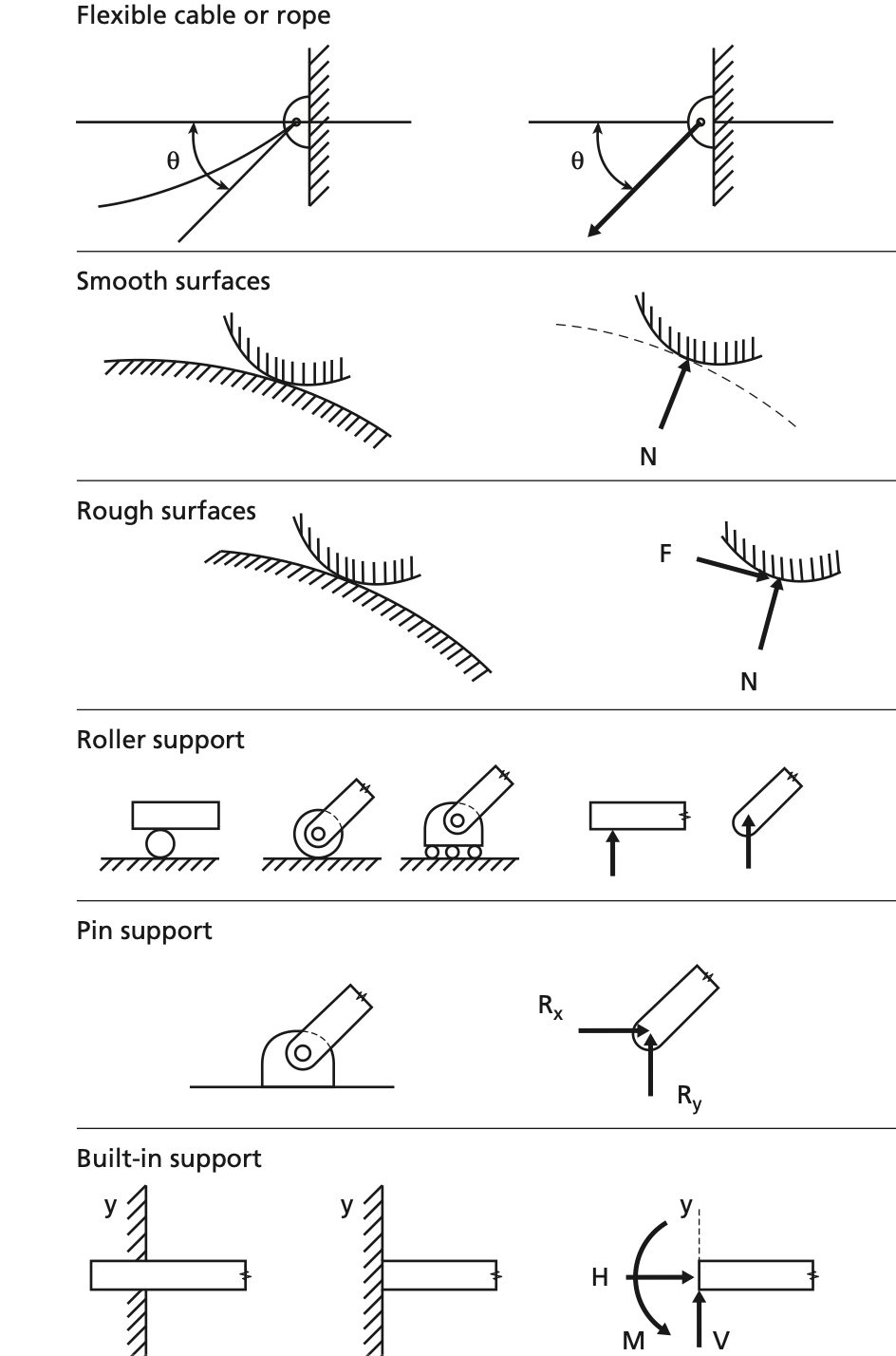
Identificar los tipos de apoyos.
Interpretar los diferentes tipos de carga y su representación geométrica
Determinar las reacciones en la vigas (simplemente apoyadas y en voladizo)
Objetivos de aprendizaje
Al final de este capítulo, debería poder:
Conocer elementos estructurales longitudinales (VIgas)
Identificar los tipos de apoyos.
Interpretar los diferentes tipos de carga y su representación geométrica
Determinar las reacciones en la vigas (simplemente apoyadas y en voladizo)
Resumen de tipos de apoyos y su representación simbólica.