Geometría
Introducción:
Intencionalmente o no, desde hace siglos, constructores, arquitectos, ingenieros han utilizado las matemáticas como una herramienta básica pero importante para el propósito del diseño, ejecución y finalización de proyectos de construcción.
En la historia, los arquitectos eran matemáticos y también algunos matemáticos también eran arquitectos.
El estudio fundamental de formas, formas y espacios y su orden junto con su geometría contribuye al proceso de composición y diseño de cualquier elemento de la arquitectura.
Intencionalmente o no, desde hace siglos, constructores, arquitectos, ingenieros han utilizado las matemáticas como una herramienta básica pero importante para el propósito del diseño, ejecución y finalización de proyectos de construcción.
En la historia, los arquitectos eran matemáticos y también algunos matemáticos también eran arquitectos.
El estudio fundamental de formas, formas y espacios y su orden junto con su geometría contribuye al proceso de composición y diseño de cualquier elemento de la arquitectura.
Fondation Louis Vuitton
- La forma del edificio, diseñada por el arquitecto Frank Gehry, que evoca unas velas ondulantes al viento, es una obra digna de admiración en sí misma.
Actividad:
Observen el siguiente video y posteriormente las imágenes de esta obra, para comentar sobre ella, desde una mirada de la matemática y su aliada la geometría, que nutre y alimenta a la arquitectura desde hace siglos.
Disfrutenla.....
Observen el siguiente video y posteriormente las imágenes de esta obra, para comentar sobre ella, desde una mirada de la matemática y su aliada la geometría, que nutre y alimenta a la arquitectura desde hace siglos.
Disfrutenla.....
Frank Gehry (izquierda) y Bernard Arnault, afuera de la Fundación Louis Vuitton en París | Imagen: Richard Grassie
Uno de los diagramas más antiguos y completos de Elementos de geometría de Euclides es un fragmento de papiro encontrado entre las pilas de basura notables de Oxyrhynchus en 1896-97 por la reconocida expedición de BP Grenfell y AS Hunt. Ahora se encuentra en la Universidad de Pennsylvania. El diagrama acompaña a la Propuesta 5 del libro II de la Elementos , y junto con otros resultados en el Libro II se puede interpretar en términos modernos como una formulación geométrica de una identidad algebraica
|
Una Mirada al Origen....
Euclides, vivió en la ciudad de Alejandría en Grecia, alrededor de 2300 años AC, pasó su vida enseñando geometría, publicó un libro llamado "Elementos" que hasta hoy en día es la base de comprensión de la geometría y procesos matemáticos. Pero claro en su contexto de visión de la matemática de esa era. Hoy sabemos que los postulados de Euclides son ciertos y uno de ellos el quinto, no lo es, pero da lugar al apasionante mundo de la geometría No Euclidiana. lo que menciono en el inicio en la presentación de esta plataforma educativa por medio de mi Avatar en el vídeo titulado: Arquitectura Virtual . |
Postulados :
1er) Dados dos puntos se pueden trazar una recta que los une.
2do) Cualquier segmento puede ser prolongado de forma continua en una recta ilimitada en la misma dirección.
3er) Se puede trazar una circunferencia de centro en cualquier punto y radio cualquiera.
4to) Todos los ángulos rectos son iguales.
5to) "La polémica": Si una recta, al cortar a otras dos, forma los ángulos internos de un mismo lado menores que dos rectos, esas dos rectas prolongadas indefinidamente se cortan del lado en el que están los ángulos menores que dos rectos.
1er) Dados dos puntos se pueden trazar una recta que los une.
2do) Cualquier segmento puede ser prolongado de forma continua en una recta ilimitada en la misma dirección.
3er) Se puede trazar una circunferencia de centro en cualquier punto y radio cualquiera.
4to) Todos los ángulos rectos son iguales.
5to) "La polémica": Si una recta, al cortar a otras dos, forma los ángulos internos de un mismo lado menores que dos rectos, esas dos rectas prolongadas indefinidamente se cortan del lado en el que están los ángulos menores que dos rectos.
- Este axioma es conocido con el nombre de axioma de las paralelas y también se enunció más tarde así:
- Por un punto exterior a una recta se puede trazar una única paralela.
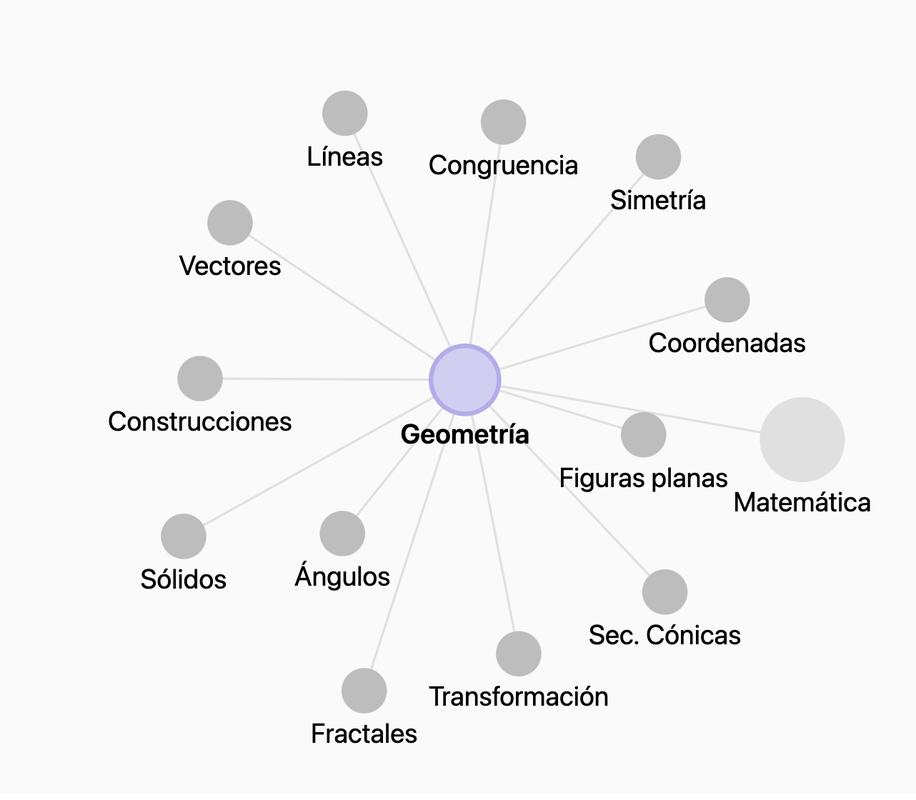
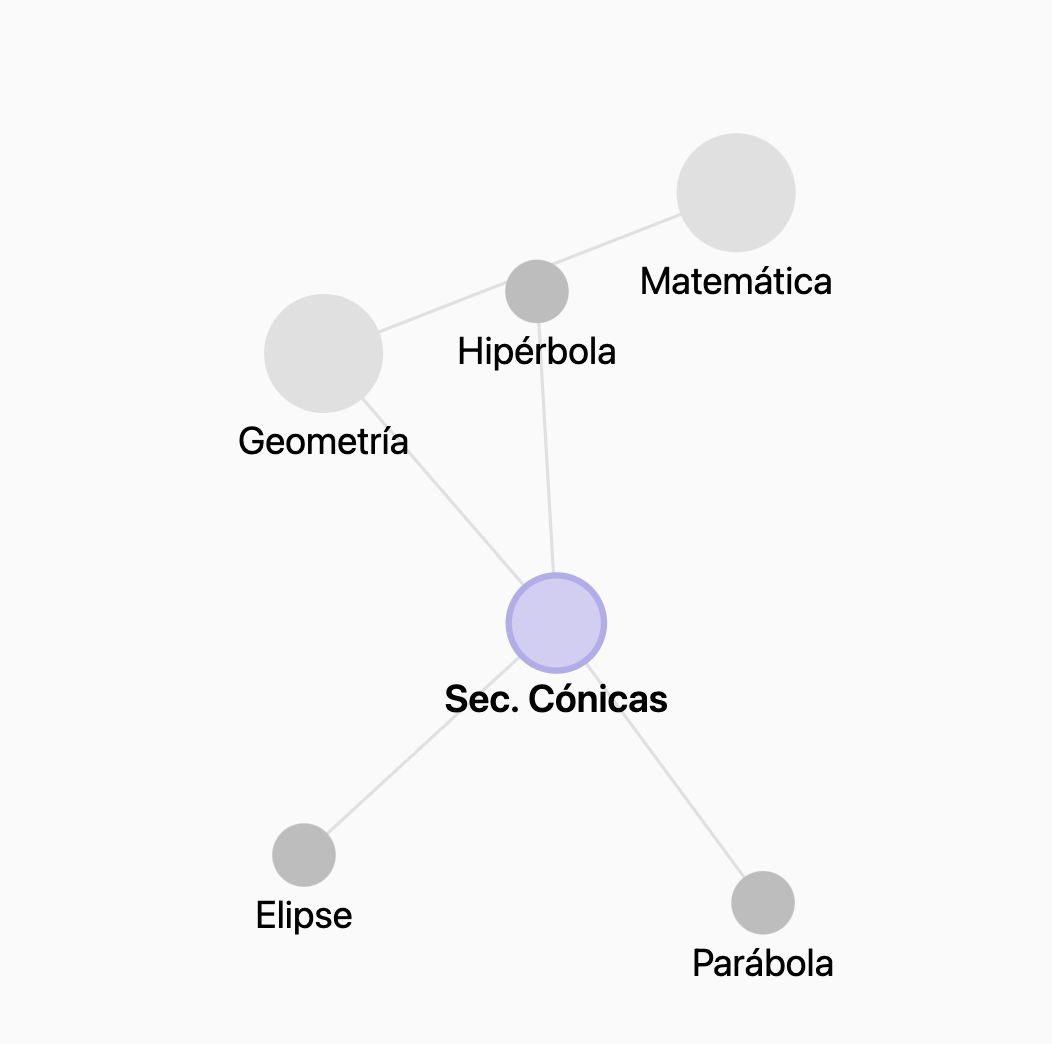
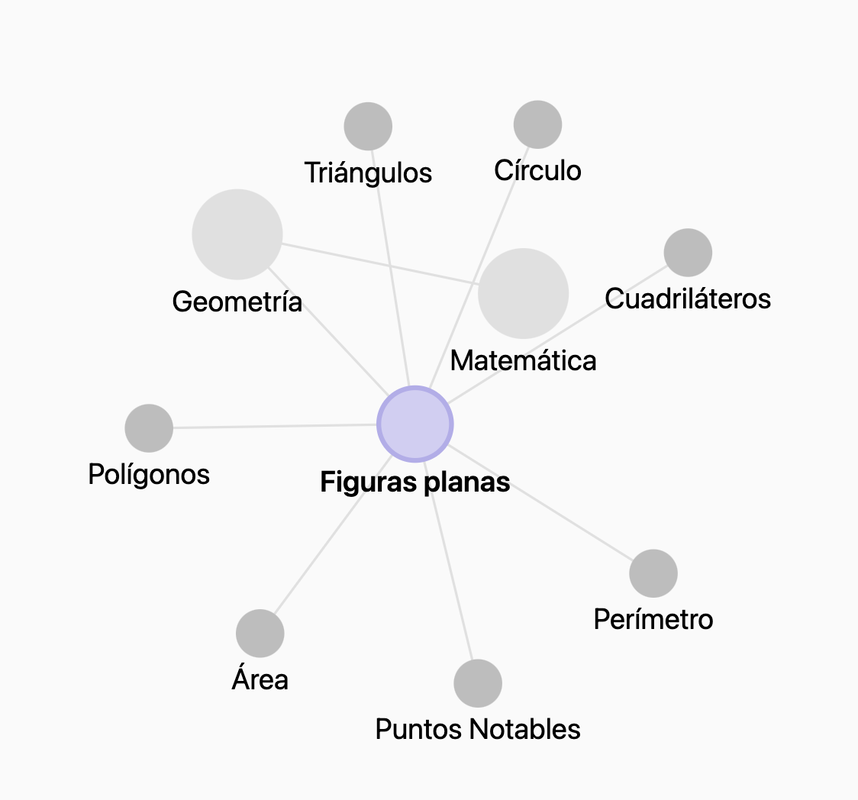
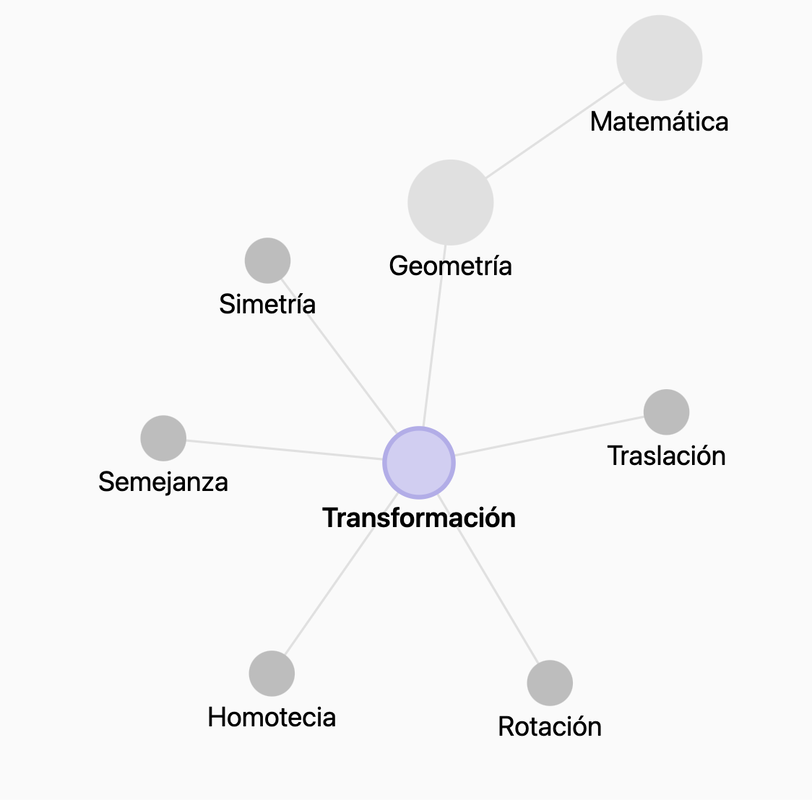
Campos de Estudio de la Geometría:
|
|
|
|
Que comience la Polémica....
¿La suma de los ángulos interiores es 180?
¿La distancia más cercana entre dos puntos es una línea recta?
¿La suma de los ángulos interiores es 180?
¿La distancia más cercana entre dos puntos es una línea recta?
HILORAMASEl hilorama es una técnica que se caracteriza por la utilización de hilos de colores, cuerdas o alambres tensados que se enrollan alrededor de un conjunto de clavos para formar figuras geométricas, abstractas u otros tipos de representaciones.
Este procedimiento se suele llevar a cabo sobre una base de madera pintada o tapizada, y con él se puede reproducir cualquier idea imaginable. Generalmente, aunque las figuras están formadas por líneas rectas, los diferentes ángulos y posiciones en el que los hilos se cruzan pueden dar la apariencia de las Curvas de Bézier. El arte del hilorama tiene su origen en las llamadas “cartas de Boole”, inventadas por Mary Everest Boole al final del siglo XIX para hacer la teoría de las matemáticas más comprensibles para los niños. Mary utilizó estas cartas para ayudar con ellas a sus alumnos a aprender la geometría de los ángulos y espacios. Esto se popularizó como un arte decorativo durante la década de 1960 mediante kits de aprendizaje y libros. |
Creación propia, por medio del Software Geogebra.
Como Construirlo:
Simple. sigue los pasos siguientes: Entra a Geogebra
|
Ejemplo:
Encontrar el punto de equilibrio entre ventas y producción:
Visto desde la Geometría
Visto desde la analítica
Conjunción de ambos métodos
Encontrar el punto de equilibrio entre ventas y producción:
Visto desde la Geometría
Visto desde la analítica
Conjunción de ambos métodos
Da lectura al siguiente artículo y comenta sobre él.
https://www.hindawi.com/journals/amse/2015/950232/#methods
https://www.hindawi.com/journals/amse/2015/950232/#methods