Funciones y Gráficas
Función:
Una función es una regla de correspondencia entre dos conjuntos de tal manera que a cada elemento del primer conjunto le corresponde uno y sólo un elemento del segundo conjunto.
Una función es una regla de correspondencia entre dos conjuntos de tal manera que a cada elemento del primer conjunto le corresponde uno y sólo un elemento del segundo conjunto.
|
Al primer conjunto (el conjunto D) se le da el nombre de dominio.
Al segundo conjunto (el conjunto C) se le da el nombre de contradominio o imágen. |
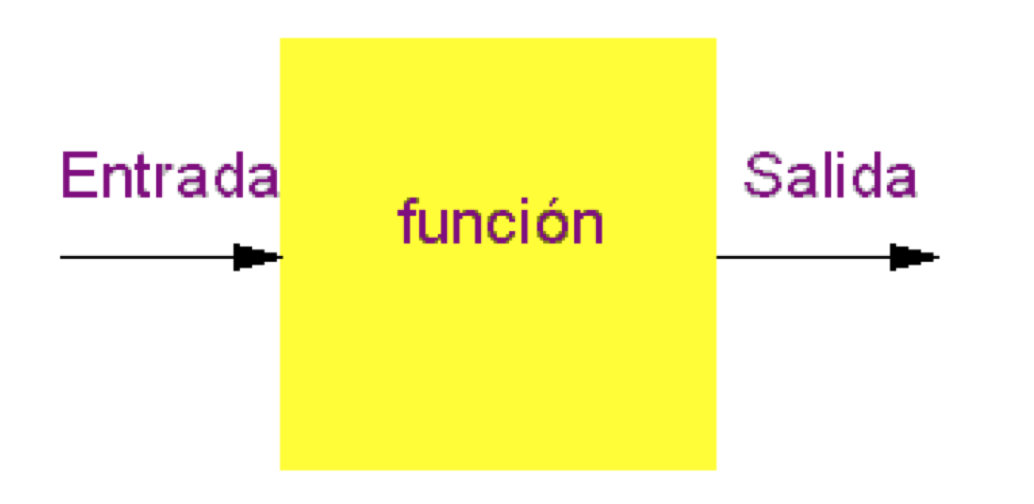
Una función se puede concebir también como un aparato de cálculo. La entrada es el dominio, los cálculos que haga el aparato con la entrada son en sí la función y la salida sería la imagen de la función.
|
|
Función como Proceso
|
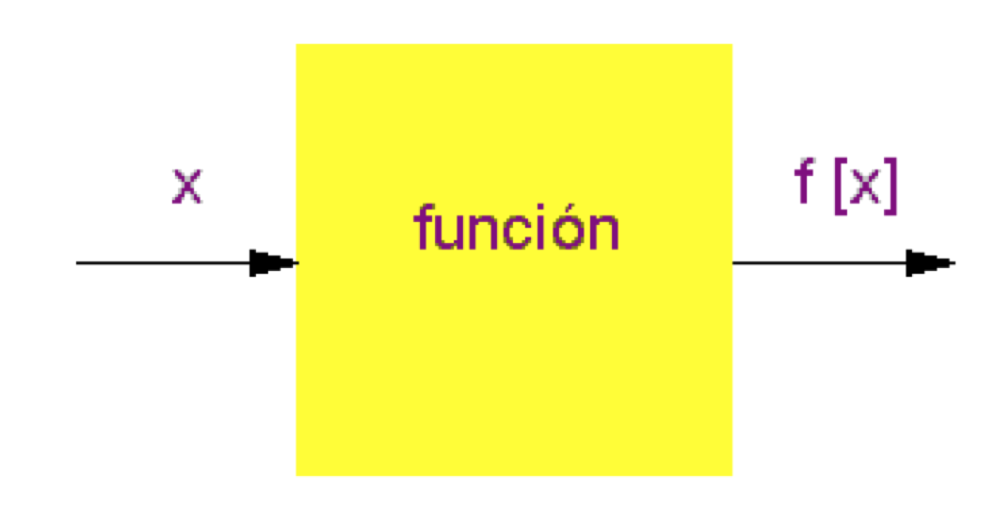
Una función f se puede también visualizar de manera intuitiva como un mecanismo que recibe como entrada un valor de x, el cual es procesado por el mecanismo, dando lugar a un valor de salida f(x) que es el valor de la variable dependiente que corresponde a x, como se ilustra en la figura.
|
Gráfica de una fución
Una función real de variable real f : A → B, se representa gráficamente por un conjunto de puntos en el plano mediante el llamado método de coordenadas de Descartes.
La gráfica de una función está formada por el conjunto de puntos (x, y) cuando x varía en el dominio D.
Para representarla calcularemos aquellos puntos o intervalos donde la función tiene un comportamiento especial, que determinaremos mediante el estudio de los siguientes apartados:
Una función real de variable real f : A → B, se representa gráficamente por un conjunto de puntos en el plano mediante el llamado método de coordenadas de Descartes.
La gráfica de una función está formada por el conjunto de puntos (x, y) cuando x varía en el dominio D.
Para representarla calcularemos aquellos puntos o intervalos donde la función tiene un comportamiento especial, que determinaremos mediante el estudio de los siguientes apartados:
- Dominio de una función.
- Simetría.
- Periodicidad.
- Puntos de corte con los ejes.
- Asíntotas.
- Ramas parabólicas.
- Crecimiento y Decrecimiento.
- Máximos y mínimos.
- Concavidad y convexidad.
Clasificación de funciones por su naturaleza
Algebraicas
y
trascendentales (Logarítmicas,Trigonométricas y Exponenciales)
Algebraicas
y
trascendentales (Logarítmicas,Trigonométricas y Exponenciales)
Trigonometría
Un poco de diversión, antes de adentrarnos en el campo de la trigonometría y recordemos "Geometría". Visita la siguiente página web del Profesor José Manuel Arranz:
Ahora comentemos sobre lo observado.
Ahora comentemos sobre lo observado.
|
Algo de Historia.....
La trigonometría simplemente significa cálculos con triángulos (de ahí proviene el tri). Es un estudio de las relaciones en matemáticas que involucran longitudes, alturas y ángulos de diferentes triángulos. El campo surgió durante el siglo III a. C., desde las aplicaciones de la geometría hasta los estudios astronómicos. La trigonometría extiende sus aplicaciones a varios campos, como arquitectos, agrimensores, astronautas, físicos, ingenieros e incluso investigadores de la escena del crimen. |
Recordando:
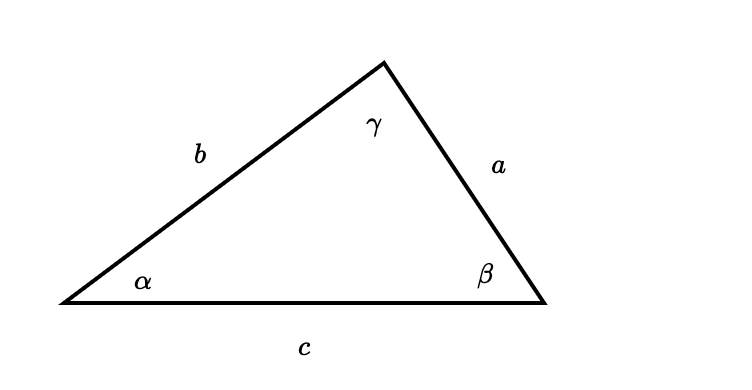
Un triángulo queda determinado cuando se dan:
1) Dos ángulos y un lado,
2) Dos lados y el ángulo comprendido entre ellos,
3) Los tres lados, siendo el mayor de ellos menor que la suma de los otros dos, y
4) Se dan dos lados y el ángulo opuesto a uno de ellos.
Un triángulo queda determinado cuando se dan:
1) Dos ángulos y un lado,
2) Dos lados y el ángulo comprendido entre ellos,
3) Los tres lados, siendo el mayor de ellos menor que la suma de los otros dos, y
4) Se dan dos lados y el ángulo opuesto a uno de ellos.
|
|
Teorema de Senos:
Nos sirve para resolver los problemas mencionados en los incisos 1) y 4)
Teorema de Coseno:
Nos sirve para resolver los problemas mencionados en los incisos 2) y 3)
Nos sirve para resolver los problemas mencionados en los incisos 1) y 4)
Teorema de Coseno:
Nos sirve para resolver los problemas mencionados en los incisos 2) y 3)
El estudio de la trigonometría se divide en:
- Trigonometría con triángulos rectángulos
- Trigonometría con triángulos generales
- Definiciones de seno, coseno y tangente a partir del círculo unitario
- Gráficas de funciones trigonométricas
- Identidades y ecuaciones trigonométricas.
Aplicaciones:
La trigonometría se puede usar para medir la altura de un edificio o montañas:
Si conoce la distancia desde donde observa el edificio y el ángulo de elevación, puede encontrar fácilmente la altura del edificio. Del mismo modo, si tiene el valor de un lado y el ángulo de depresión desde la parte superior del edificio que puede encontrar y otro lado en el triángulo, todo lo que necesita saber es un lado y ángulo del triángulo.
Trigonometría en videojuegos:¿Alguna vez has jugado el juego, Mario? Cuando lo veas, deslízate suavemente sobre los obstáculos. Realmente no salta recto a lo largo del eje Y, es un camino ligeramente curvado o un camino parabólico que toma para abordar los obstáculos en su camino. La trigonometría ayuda a Mario a saltar estos obstáculos. Como saben, la industria del juego tiene que ver con trigonometría y las computadoras, por lo tanto, la trigonometría es de igual importancia para estas ingenierias.
Trigonometría en la arquitectura edificada:
En la construcción necesitamos trigonometría para calcular lo siguiente:
La trigonometría se puede usar para medir la altura de un edificio o montañas:
Si conoce la distancia desde donde observa el edificio y el ángulo de elevación, puede encontrar fácilmente la altura del edificio. Del mismo modo, si tiene el valor de un lado y el ángulo de depresión desde la parte superior del edificio que puede encontrar y otro lado en el triángulo, todo lo que necesita saber es un lado y ángulo del triángulo.
Trigonometría en videojuegos:¿Alguna vez has jugado el juego, Mario? Cuando lo veas, deslízate suavemente sobre los obstáculos. Realmente no salta recto a lo largo del eje Y, es un camino ligeramente curvado o un camino parabólico que toma para abordar los obstáculos en su camino. La trigonometría ayuda a Mario a saltar estos obstáculos. Como saben, la industria del juego tiene que ver con trigonometría y las computadoras, por lo tanto, la trigonometría es de igual importancia para estas ingenierias.
Trigonometría en la arquitectura edificada:
En la construcción necesitamos trigonometría para calcular lo siguiente:
- Medición de predios, lotes;
- Hacer paredes paralelas, perpendiculares e inclinadas.
- Instalación de pisos cerámicos;
- Calcular la inclinación del techo para su correcto funcionamiento ante climas imperantes en el lugar de construcción;
- La altura del edificio, la longitud del ancho, etc. y muchas otras cosas en las que se hace necesario usar trigonometría.
Las funciones trigonométricas:
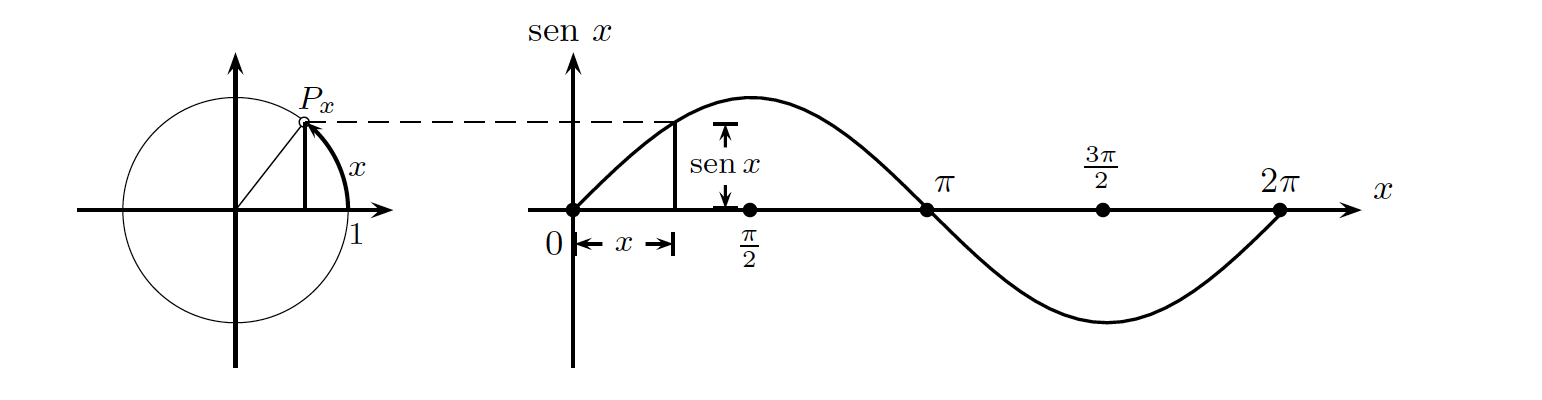
Consideremos en un plano cartesiano la circunferencia de centro el origen y radio unitario. Para cada número real x, consideremos el arco de circunferencia de longitud x, con extremo el punto inicial A = (1, 0). Sea Px el extremo final del arco ⌢ APx de longitud x.
Se definen las funciones seno y coseno de la forma siguiente:
sen : R → [−1, 1], sen x = ordenada de Px
y
cos : R → [−1, 1], cos x = abscisa de Px.
Consideremos en un plano cartesiano la circunferencia de centro el origen y radio unitario. Para cada número real x, consideremos el arco de circunferencia de longitud x, con extremo el punto inicial A = (1, 0). Sea Px el extremo final del arco ⌢ APx de longitud x.
Se definen las funciones seno y coseno de la forma siguiente:
sen : R → [−1, 1], sen x = ordenada de Px
y
cos : R → [−1, 1], cos x = abscisa de Px.
Gráfica de las funciones seno y coseno, realizado en la plataforma Geogebra
Círculo Trigonométrico
|
Tabla de valores de las funciones trigonométricas.
tomado de :http://www.knowledgehi.com/Facts/blueprints/blueprints_mathematics_trigonometry_1600x900_wallpaper_719 |
|
Trigonometría Gráfica en 3D
Video de funciones sinusoidales
https://player.vimeo.com/video/65475425
https://player.vimeo.com/video/170587058
https://player.vimeo.com/video/65475425
https://player.vimeo.com/video/170587058