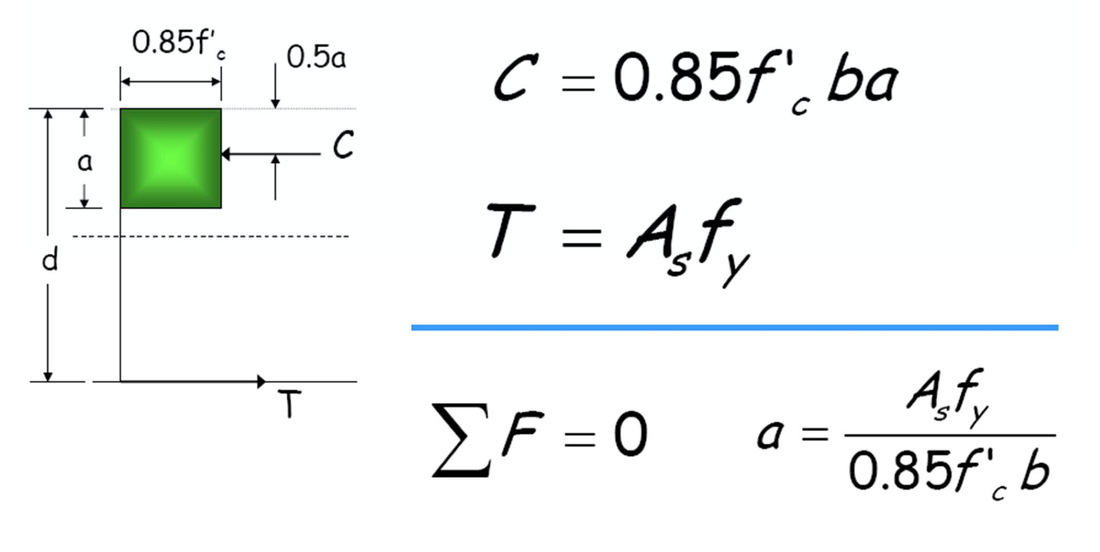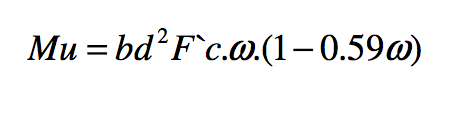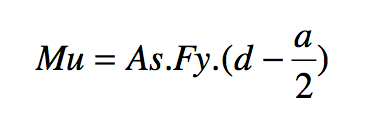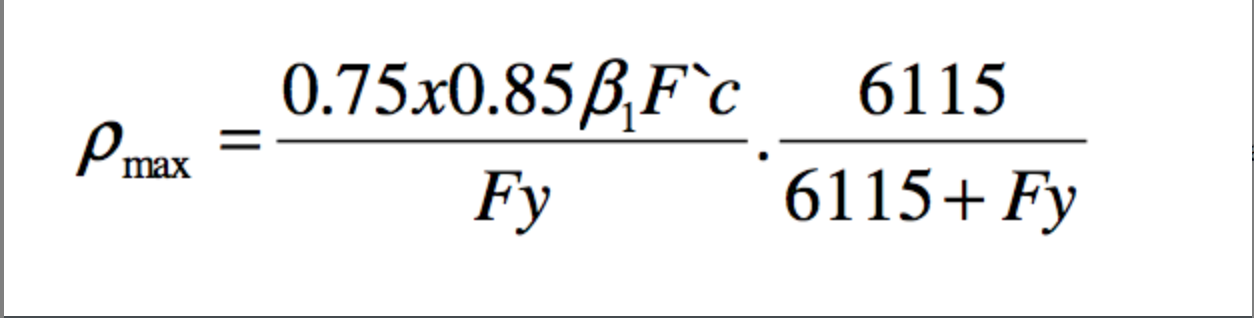Módulo II. Diseño de Vigas.
Lo que sabes y lo que aprenderás en esta asignatura:
Sabes:
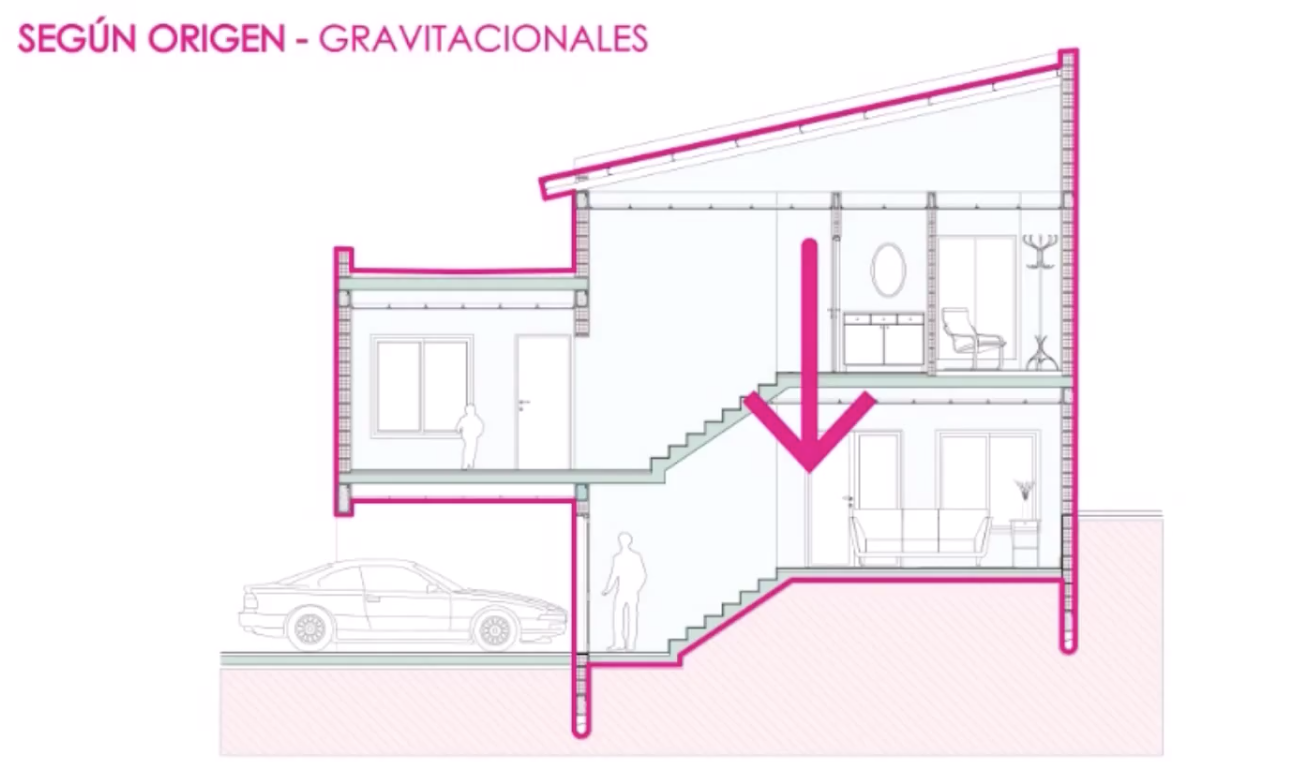
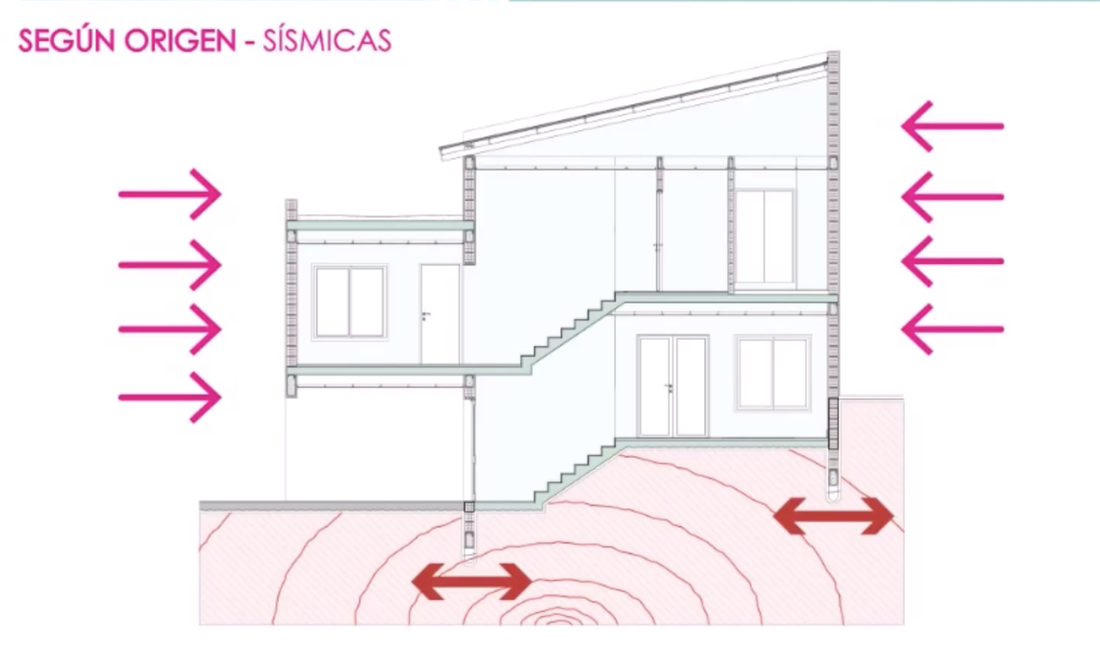
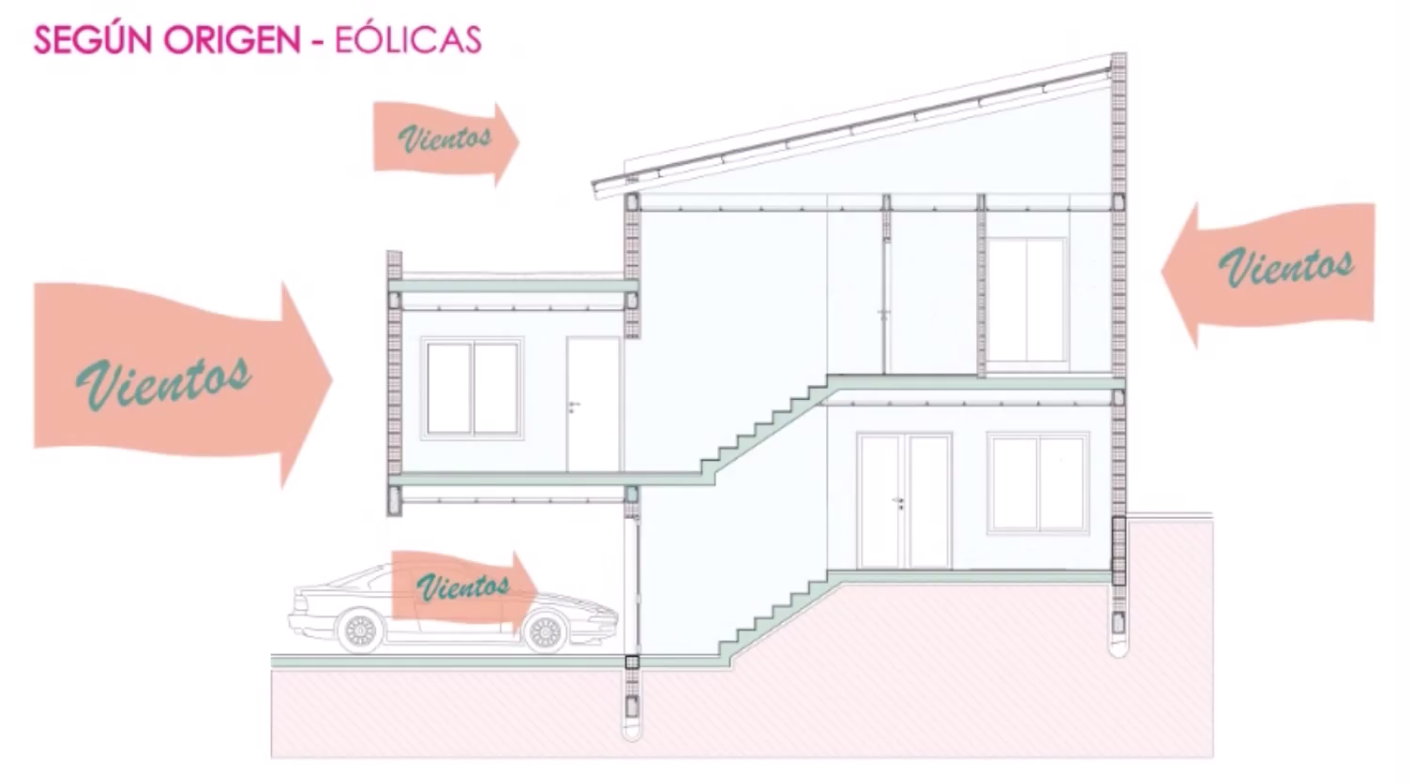
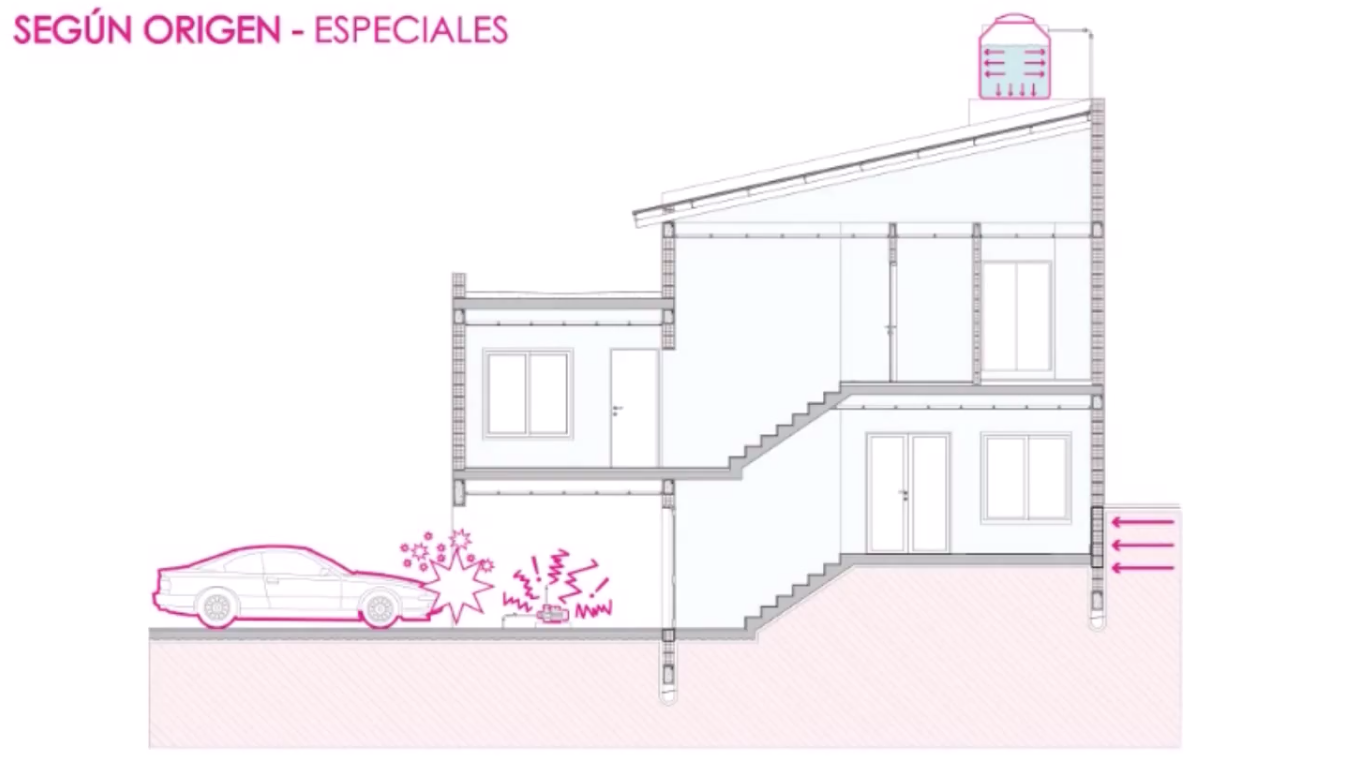
Los Tipos de Cargas, Origen y Clasificación.
Concentradas
Uniformemente distribuidas
Uniformemente variadas
Momentos
Sabes:
Los Tipos de Cargas, Origen y Clasificación.
Concentradas
Uniformemente distribuidas
Uniformemente variadas
Momentos
|
|
|
|
|
|
Calculo de magnitudes de cargas sobre elementos estructúrales
(vigas, losas, columnas, cimentación)
(vigas, losas, columnas, cimentación)
Peso y Carga sobre Viga (Metro2, 20201)
|
Carga sobre entrepiso (Metro2, 2021)
|
Obtención de elementos mecánicos en vigas y marcos
Calculo de reacciones en vigas isostática e hiperestática
Calculo de Fuerzas Cortantes
Calculo de Momentos máximo
Calculo de reacciones en vigas isostática e hiperestática
Calculo de Fuerzas Cortantes
Calculo de Momentos máximo
Diagramas de Fuerza Cortante y Momento Flexionante, (Guzmán 2021)
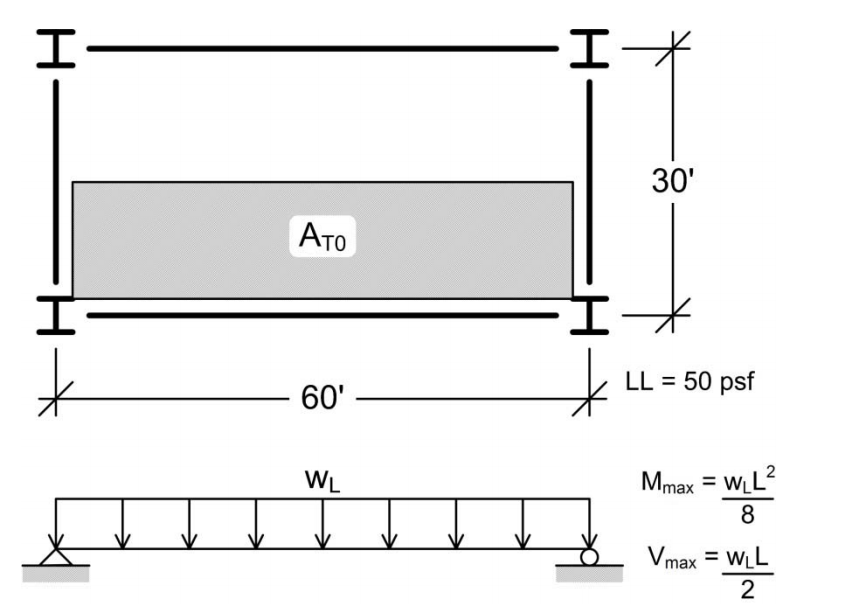
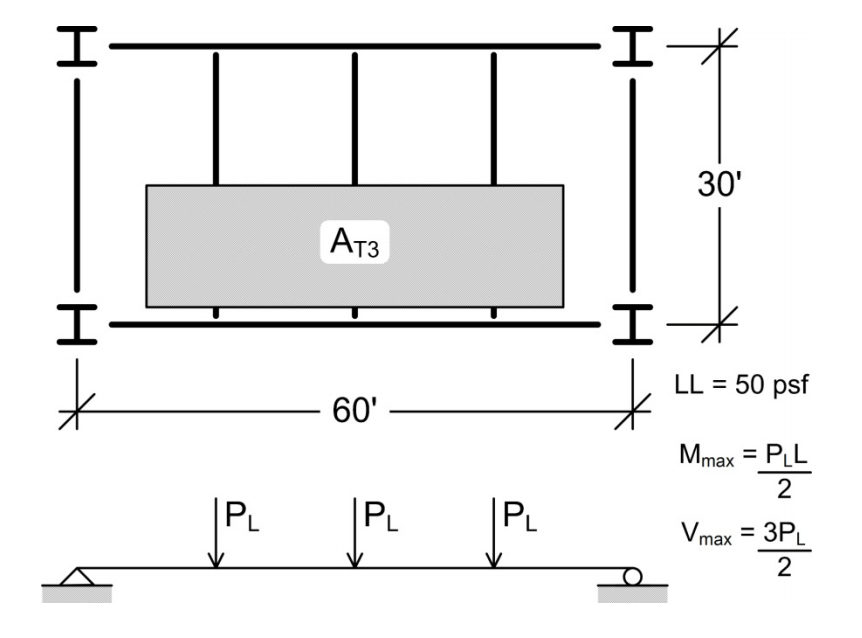
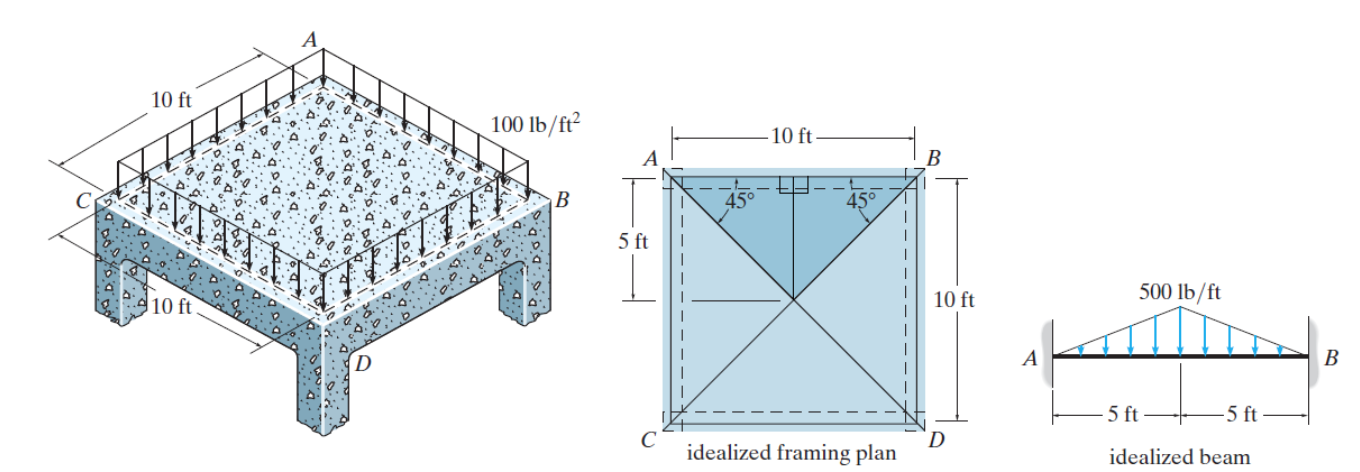
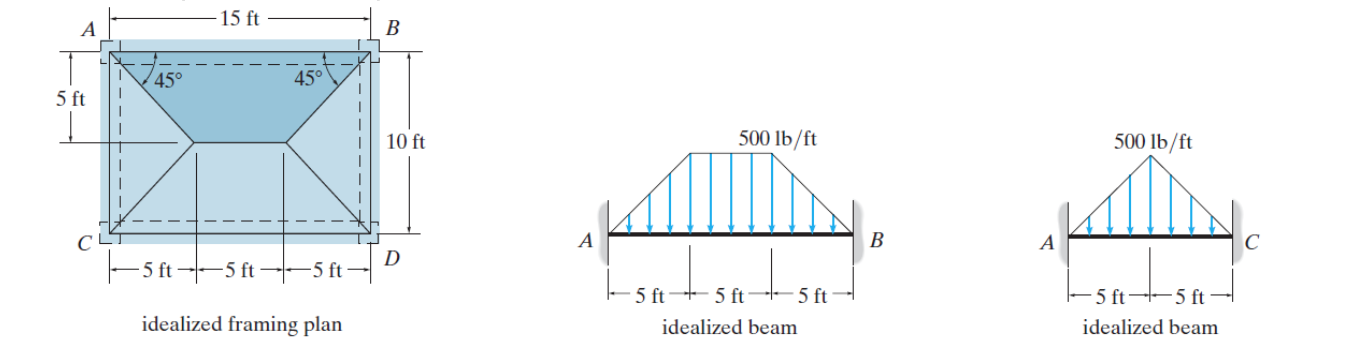
Bajada de cargas por el método de área tributaría
En tableros de sistemas de entrepiso y cubiertas
Columnas centrales, esquina, intermedias.
Vigas secundarias
Vigas principales
En tableros de sistemas de entrepiso y cubiertas
Columnas centrales, esquina, intermedias.
Vigas secundarias
Vigas principales
|
|
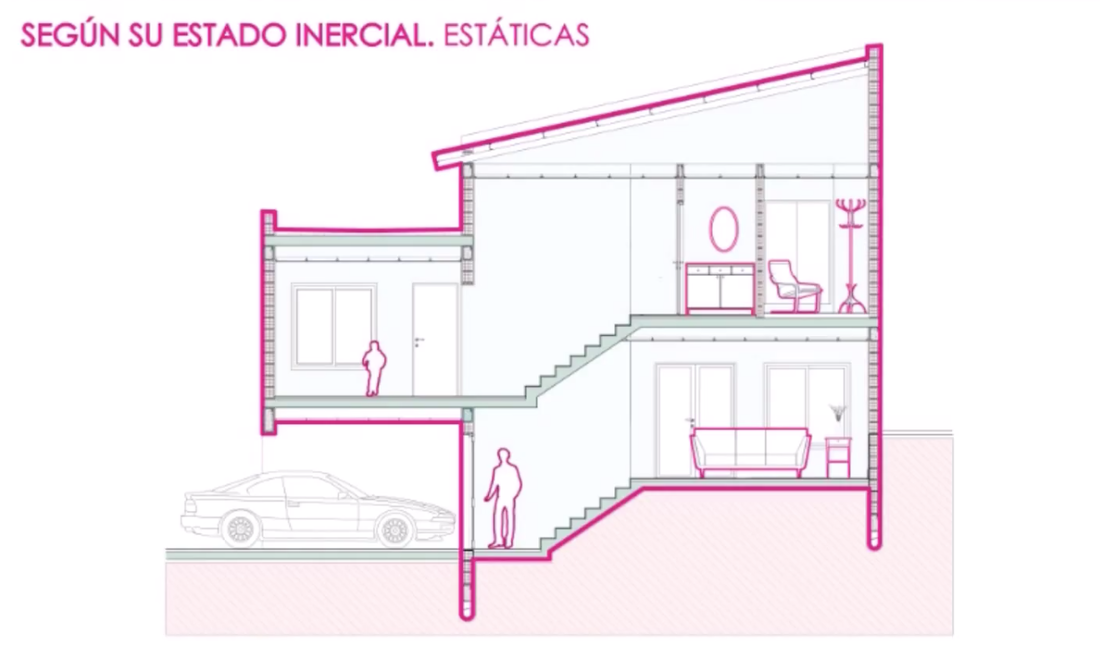
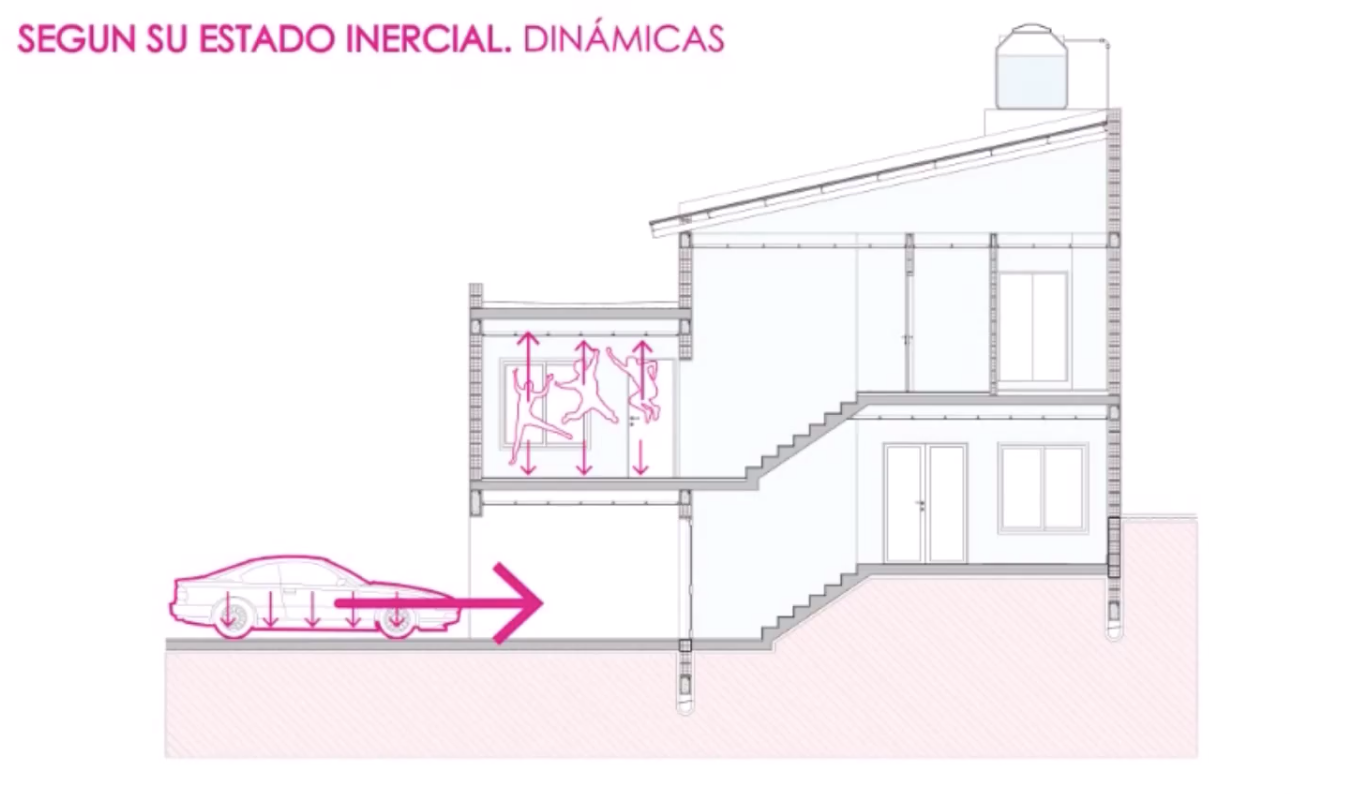
Sistema Estructural
Museo Nacional de Qatar (2019) de Jean Nouvel (Doha, Qatar)
|
(elementos que lo integran):
|
Lo que Aprenderás:
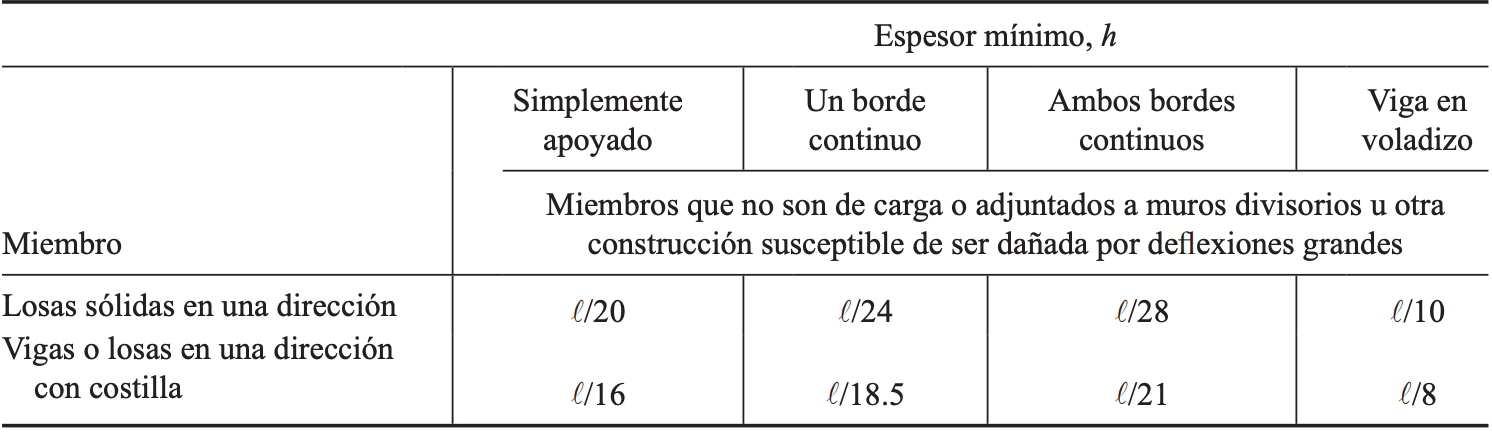
Pre dimensionar una viga de concreto
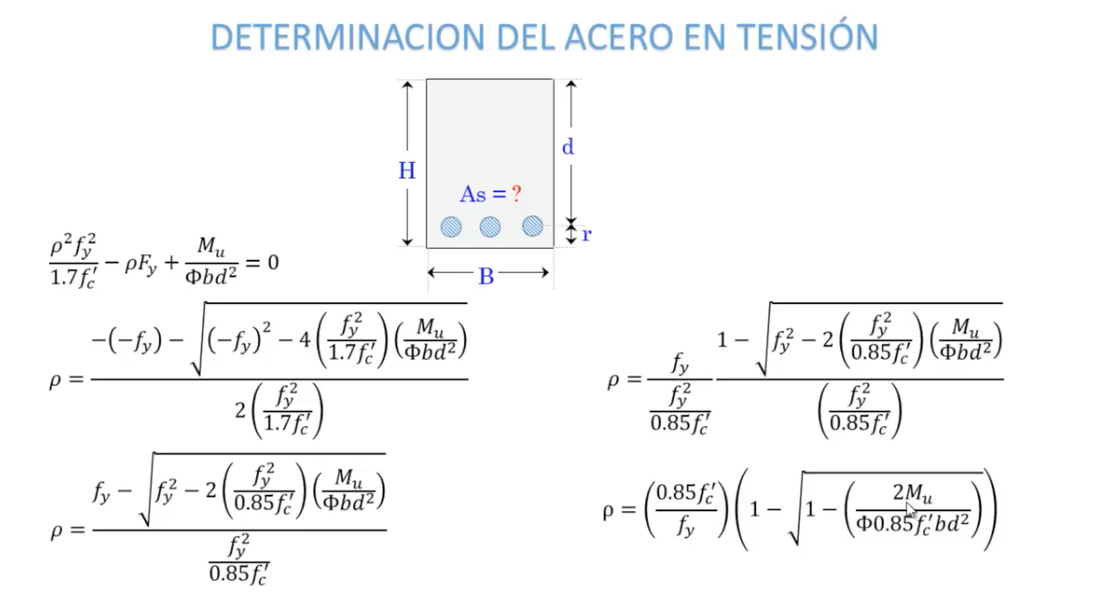
Calcular su área de acero para resistir momentos flexionantes
Calcular el área de acero para soportar esfuerzos cortantes
Planos estructurales y croquis.
Pre dimensionar una viga de concreto
Calcular su área de acero para resistir momentos flexionantes
Calcular el área de acero para soportar esfuerzos cortantes
Planos estructurales y croquis.
Infografia viga reforzada, recuperado de: https://es.pinterest.com/pin/365706432227498778/
Simplemente Reforzada.
Filosofía de diseño.
Diseño por Estados Límites de Resistencia y Servicio. (LRFD)
Tanto en el caso de las edificaciones como en el de las estructuras para la arquitectura edificada (obra civil) es necesario, no solo satisfacer la resistencia, se debe proporcionar otras previsiones tales como: Suficiente rigidez , para tener deflexiones aceptables, ductilidad apropiada, para permitir que en caso de cargar la estructura hasta la falla, esta se presente de forma controlada y diferida en el tiempo (Uribe, 2000).
Lo anterior se puede lograr al evaluar las posibles condiciones que llevan a una estructura a perder su funcionalidad (sus elementos alcanzan su capacidad portante, exceder las deformaciones). A estas condiciones se les denomina estados límite de resistencia y estados límite de servicio.
Filosofía de diseño.
Diseño por Estados Límites de Resistencia y Servicio. (LRFD)
Tanto en el caso de las edificaciones como en el de las estructuras para la arquitectura edificada (obra civil) es necesario, no solo satisfacer la resistencia, se debe proporcionar otras previsiones tales como: Suficiente rigidez , para tener deflexiones aceptables, ductilidad apropiada, para permitir que en caso de cargar la estructura hasta la falla, esta se presente de forma controlada y diferida en el tiempo (Uribe, 2000).
Lo anterior se puede lograr al evaluar las posibles condiciones que llevan a una estructura a perder su funcionalidad (sus elementos alcanzan su capacidad portante, exceder las deformaciones). A estas condiciones se les denomina estados límite de resistencia y estados límite de servicio.
Este método se basa en diseñar los elementos de una estructura para que resistan cargas mayores a las de servicio de manera que se considera la resistencia o la condición de falla. En forma matemática la relación que describe el método es la siguiente: (Rochel Awad, 2007)
Ru≤ ΦRn Ecuación (1), Donde:
Ru: Es la carga factorizada.
Rn: Es la resistencia nominal de los materiales.
Φ: Es el factor de resistencia dado por las especificaciones para cada estado límite, los cuales son generalmente valores inferiores a la unidad.
Ru≤ ΦRn Ecuación (1), Donde:
Ru: Es la carga factorizada.
Rn: Es la resistencia nominal de los materiales.
Φ: Es el factor de resistencia dado por las especificaciones para cada estado límite, los cuales son generalmente valores inferiores a la unidad.
¿POR QUÉ SE ESTABLECE UN ESTADO LIMITE?
“Se establece para definir un evento que puede hacer que la estructura o uno de sus elementos se vuelva inservible desde el punto de vista de su función origina.
Estados Límites:
Se denomina estado límite de una estructura o elemento estructural cuando llega al límite de su uso programado. Para las estructuras de concreto podemos considerar los siguientes estados límites (Segura Franco, 2011):
Estado límite de falla: Corresponde al colapso parcial o total de una estructura con características como la pérdida de equilibrio total o parcial, la rotura del elemento o de los elementos principales o básicos que conduzcan al colapso, la falla progresiva por diferentes motivos, la formación de mecanismos plásticos y la fatiga del material.
Estado límite de servicio: Corresponde a la interrupción del uso de la estructura, sin que conlleve al colapso, por factores como deflexiones excesivas, fisuras o grietas importantes, o vibraciones excesivas.
Estados límites especiales: Corresponden a daños o fallas debidos a condiciones especiales como movimientos sísmicos anormales, intervención del fuego, explosiones, colisiones de diverso tipo, corrosión, deterioro por factores no contemplados en el diseño.
“Se establece para definir un evento que puede hacer que la estructura o uno de sus elementos se vuelva inservible desde el punto de vista de su función origina.
Estados Límites:
Se denomina estado límite de una estructura o elemento estructural cuando llega al límite de su uso programado. Para las estructuras de concreto podemos considerar los siguientes estados límites (Segura Franco, 2011):
Estado límite de falla: Corresponde al colapso parcial o total de una estructura con características como la pérdida de equilibrio total o parcial, la rotura del elemento o de los elementos principales o básicos que conduzcan al colapso, la falla progresiva por diferentes motivos, la formación de mecanismos plásticos y la fatiga del material.
Estado límite de servicio: Corresponde a la interrupción del uso de la estructura, sin que conlleve al colapso, por factores como deflexiones excesivas, fisuras o grietas importantes, o vibraciones excesivas.
Estados límites especiales: Corresponden a daños o fallas debidos a condiciones especiales como movimientos sísmicos anormales, intervención del fuego, explosiones, colisiones de diverso tipo, corrosión, deterioro por factores no contemplados en el diseño.
Material de Consulta (Lectura Obligada):
Combinaciones de Carga.
Cargas Se calculan con la norma American Society of Civil Engineers (ASCE) 7- «Minimum Design Loads for Buildings and Other Structures», la cual define estados de carga para diseño en concreto, madera y acero en edificios (no se aplica a puentes).
La última versión de esta norma es del 2010, pero la que define las cargas de viento con un período de retorno similar a la norma UNIT 50-84 es la de ASCE 7-2005.
Define 4 categorías de edificios según su uso y destino.
Combinaciones de carga –LRFD
U= 1.4(D + F)
U= 1.2(D + F + T)+1.6(L + H)+0.5(Lr o S o R)
U= 1.2D +1.6(Lr o S o R)+(1.0L o 0.8W)
U = 1.2D +1.6W +1.0L +0.5(Lr o S o R)
U = 1.2D +1.0E +1.0L +0.2S
U = 0.9D +1.6W +1.6H
U= 0.9D +1.0E +1.6H
Donde:
U = carga de diseño o última que la estructura necesita poder resistir
D = carga muerta
F = cargas debidas al peso y presión de fluidos
T = efectos totales de la temperatura, flujo, contracción, asentamientos diferenciales y concreto compensador de la contracción
L = carga viva
H = cargas debidas al peso y a la presión lateral del suelo, presión del agua subterránea o presión de materiales a granel
Lr = carga viva de techo
S = carga de nieve
R = carga pluvial
W = carga eólica
E = efectos sísmicos o de carga de terremoto
Cargas Se calculan con la norma American Society of Civil Engineers (ASCE) 7- «Minimum Design Loads for Buildings and Other Structures», la cual define estados de carga para diseño en concreto, madera y acero en edificios (no se aplica a puentes).
La última versión de esta norma es del 2010, pero la que define las cargas de viento con un período de retorno similar a la norma UNIT 50-84 es la de ASCE 7-2005.
Define 4 categorías de edificios según su uso y destino.
Combinaciones de carga –LRFD
U= 1.4(D + F)
U= 1.2(D + F + T)+1.6(L + H)+0.5(Lr o S o R)
U= 1.2D +1.6(Lr o S o R)+(1.0L o 0.8W)
U = 1.2D +1.6W +1.0L +0.5(Lr o S o R)
U = 1.2D +1.0E +1.0L +0.2S
U = 0.9D +1.6W +1.6H
U= 0.9D +1.0E +1.6H
Donde:
U = carga de diseño o última que la estructura necesita poder resistir
D = carga muerta
F = cargas debidas al peso y presión de fluidos
T = efectos totales de la temperatura, flujo, contracción, asentamientos diferenciales y concreto compensador de la contracción
L = carga viva
H = cargas debidas al peso y a la presión lateral del suelo, presión del agua subterránea o presión de materiales a granel
Lr = carga viva de techo
S = carga de nieve
R = carga pluvial
W = carga eólica
E = efectos sísmicos o de carga de terremoto
Fuente:
1 International Code Council, 2006 International Building Code Falls Church, Virginia 22041-3401, 755 páginas.
2 American Society of Civil Engineers, Minimum Design Loads for Buildings and Other Structures. ASCE 7-05 (Reston, VA: American Society of Civil Engineers), pág. 5.
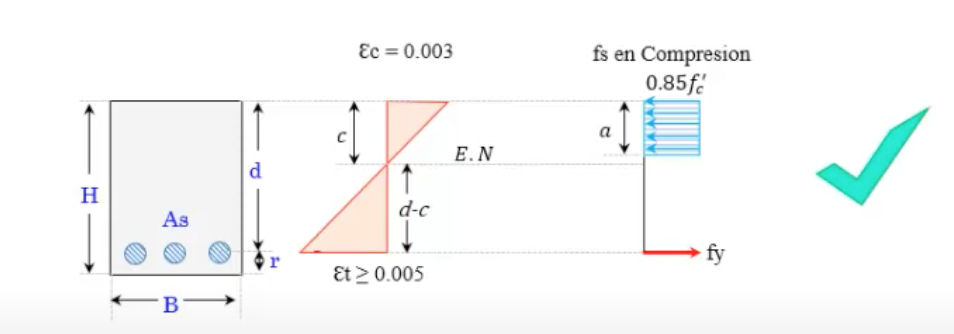
Hipótesis de Diseño 1 (ACI)
1) Las deformaciones en el refuerzo y en el concreto se suponen directamente proporcionales a la distancia desde el eje neutro (ACI, 10.2.2).
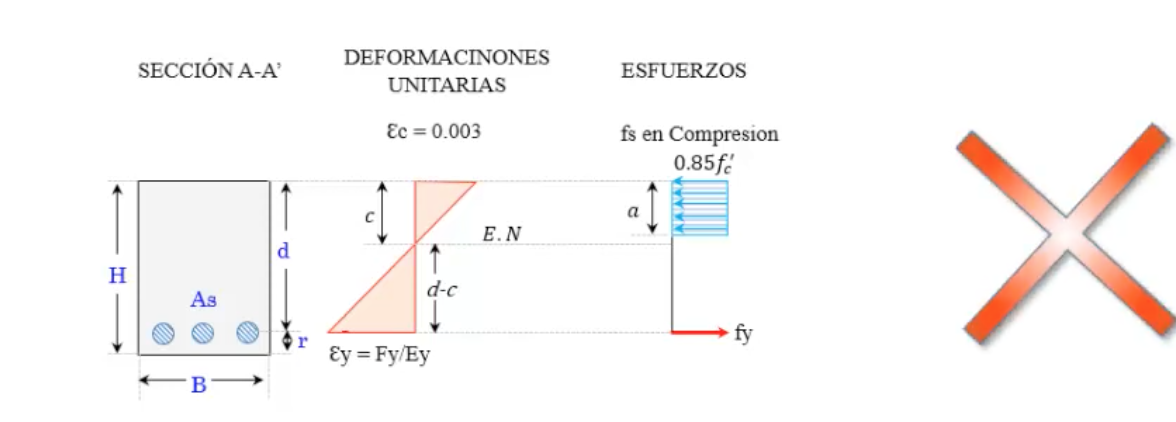
2) La máxima deformación utilizable en la fibra extrema en compresión del concreto se supondrá u = 0.003 (ACI, 10.2.3).
3) El esfuerzo del acero de refuerzo fs inferior a la resistencia a la fluencia fy, debe tomarse como Es veces la deformación unitaria del refuerzo Es . Para deformaciones mayores que fy/Es , el esfuerzo en el acero de refuerzo será considerado independiente de la deformación e igual a fy (ACI, 10.2.4).
4) La resistencia a la tensión del concreto no es considerada en el cálculo de la resistencia a flexión del concreto reforzado (ACI, 10.2.5).
5 ) La relación entre la distribución del esfuerzo por compresión en el concreto y su deformación unitaria se puede suponer que es rectangular, trapezoidal, parabólica o cualquier otra forma que resulte en la predicción de la resistencia que concuerde con los resultados de pruebas (ACI, 10.2.6).
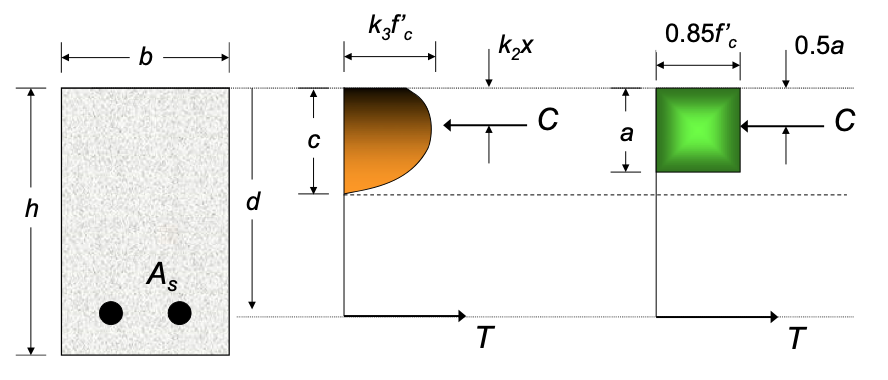
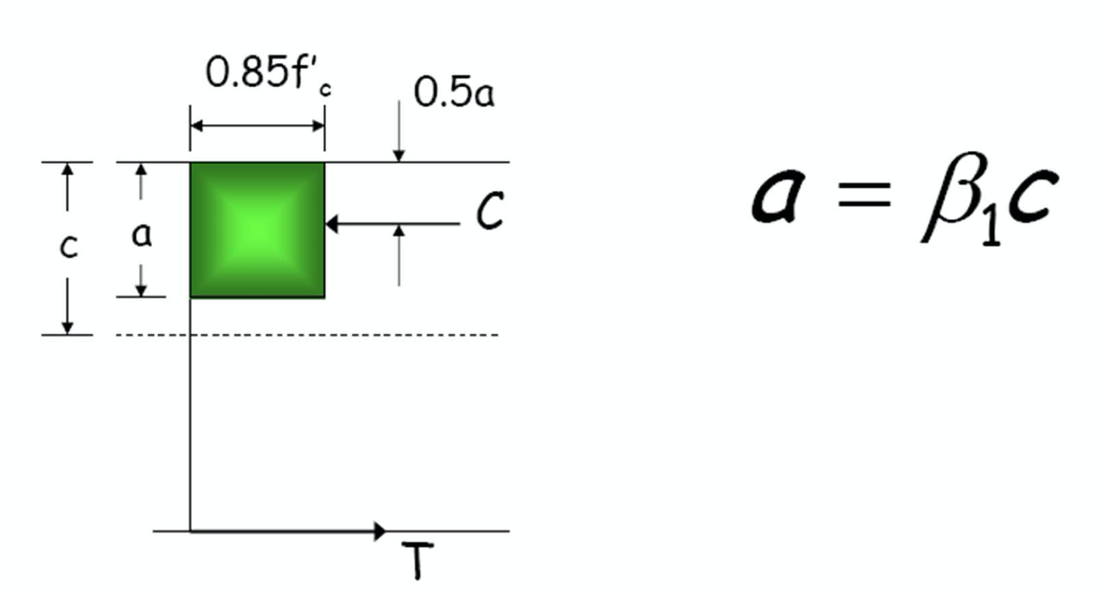
6) Los requisitos de la hipótesis #5 pueden considerarse satisfechos si se emplea una distribución rectangular equivalente de esfuerzos del concreto definida como sigue: un esfuerzo en el concreto de 0.85f’c se supondrá de manera uniformemente distribuido en una zona de compresión equivalente que esté limitada por los extremos de la sección transversal y una línea recta paralela al eje neutro, a una distancia a = (b1c) a partir de la fibra de deformación máxima en compresión. La distancia c desde la fibra de deformación máxima en compresión al eje neutro debe ser medida en dirección perpendicular a dicho eje. El factor (b1) deberá tomarse como 0.85 para resistencias f’c hasta de 280 kg/cm2 , y debe reducirse de manera uniforme en 0.05 por cada 70 kg/cm2 de aumento por sobre 280 kg/cm2 , pero no debe ser menor que 0.65 , ver tabla 22.2.2.4.3 (ACI, 10.2.7).
Hipótesis de diseño 2
Las hipótesis del método de los estados límites de resistencia, se fundamenta en las siguientes hipótesis, y los ensayos que las verifican (Rochel Awad, 2007)
Las hipótesis del método de los estados límites de resistencia, se fundamenta en las siguientes hipótesis, y los ensayos que las verifican (Rochel Awad, 2007)
- Se admite que las secciones planas antes de la flexión, permanecen planas después de que la sección se deforme, es decir que las deformaciones son proporcionales a su distancia al eje neutro.
- No se considera el diagrama de compresión del concreto como rectilíneo, por lo que no se acepta la proporcionalidad entre deformación y tensión del mismo.
- Admite la adherencia perfecta entre la interfaz del concreto y el acero dado que las varillas usadas hoy en día son corrugadas y garantizan en gran proporción dicha hipótesis.
- Se considera despreciable el aporte del concreto a tracción, hipótesis que no influye apreciablemente en la exactitud de los resultados.
- Resultados experimentales en vigas demuestran que la deformación del concreto en el instante de la falla o rotura (fisura), εut, varía entre 0.0032 y 0.0037 para concretos de 140 a 350 kgf /cm2, por lo que se asume un valor más conservador y seguro de magnitud de 0.003.
Fuente: ACI_318_14
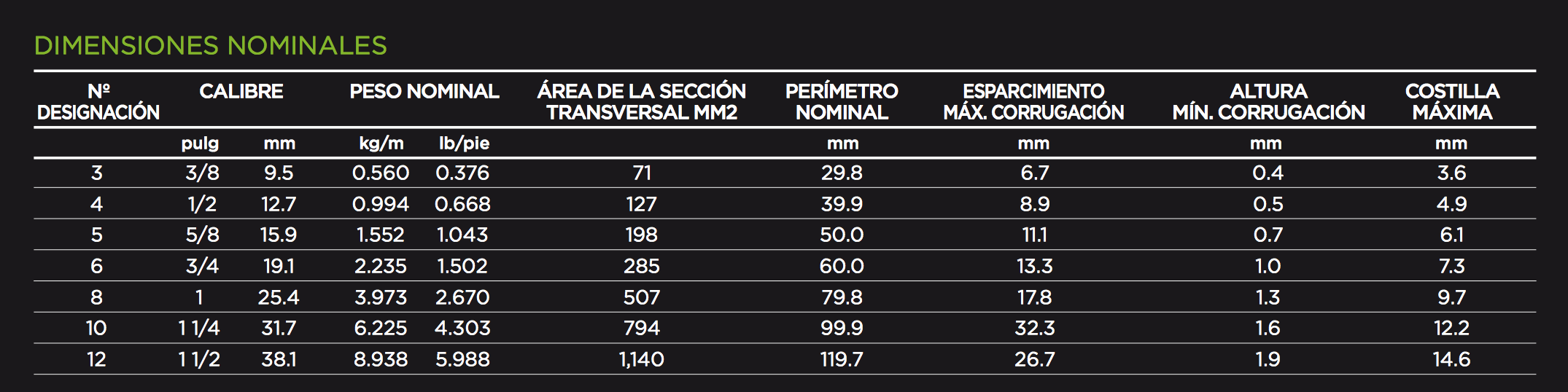
Propiedades geométricas de las varillas
|
|
Área de la sección transversal por número de varilla en centimetros cuadrados
|
Área de la sección transversal por número de varilla en pulgadas cuadradas
|
Recordar: Factor de conversión de pl2 a cm2 :
1 cm2 = 1 pl2/ 0.155
Infografia detalle de armado de refuerzo en viga, recuperado de: https://es.pinterest.com/pin/365706432227498778/
Fuente: Secciones transversales para Pre Dimencionamiento (McCormac, 2015)
Viga de Concreto Reforzado, Rectangular, con barras de refuerzo de acero (Varillas), Tomado de : https://skyciv.com/, Febrero 2020
Actividad a realizar en esta unidad de aprendizaje:
1) De tu proyecto de Composición Arquitectónica, del semestre inmediato anterior, identificar las trabes (vigas) que contiene, construyendo un plano donde las indiquen.
2) Analizar la cargas (muerta y viva) que actúa sobre la viga crítica (la de mayor longitud), por medio del sistema de bajada de cargas y área tributaria, tomarás para ello el plano de acabados donde estableciste los materiales, el sistema de entrepiso o cubierta, así como tipo de muros, indicarán en un plano la magnitud de la carga por metro lineal. Indicando la carga viva conforme lo establecido en el Reglamento de Construcción de acuerdo al uso y destino del proyecto.
3) Factorizar las cargas, acorde a lo indicado en las Normas Técnicas Complementarias de la ciudad de México o el Reglamento de Construcción del Estado de Michoacán.
4) Con ayuda de algún programa o con las herramientas adquiridas en el desarrollo de tu aprendizaje, encontrar las esfuerzos (Cortante y Momento Flexionante) de la viga indicada en el numeral 2, dibujando sus diagramas y los colocando los valores máximos.
5) Los planos y la memoria técnica lo subirás en el Enlace para subir tareas. (carpetas Drive de Google)
Actividad a realizar en esta unidad de aprendizaje:
1) De tu proyecto de Composición Arquitectónica, del semestre inmediato anterior, identificar las trabes (vigas) que contiene, construyendo un plano donde las indiquen.
2) Analizar la cargas (muerta y viva) que actúa sobre la viga crítica (la de mayor longitud), por medio del sistema de bajada de cargas y área tributaria, tomarás para ello el plano de acabados donde estableciste los materiales, el sistema de entrepiso o cubierta, así como tipo de muros, indicarán en un plano la magnitud de la carga por metro lineal. Indicando la carga viva conforme lo establecido en el Reglamento de Construcción de acuerdo al uso y destino del proyecto.
3) Factorizar las cargas, acorde a lo indicado en las Normas Técnicas Complementarias de la ciudad de México o el Reglamento de Construcción del Estado de Michoacán.
4) Con ayuda de algún programa o con las herramientas adquiridas en el desarrollo de tu aprendizaje, encontrar las esfuerzos (Cortante y Momento Flexionante) de la viga indicada en el numeral 2, dibujando sus diagramas y los colocando los valores máximos.
5) Los planos y la memoria técnica lo subirás en el Enlace para subir tareas. (carpetas Drive de Google)
VIGAS RECTANGULARES SIMPLEMENTE ARMADAS
Una viga de concreto es rectangular, cuando su sección transversal en compresión tiene esa forma. Es simplemente armada, cuando sólo tiene refuerzo para tomar la componente de tensión del par interno.
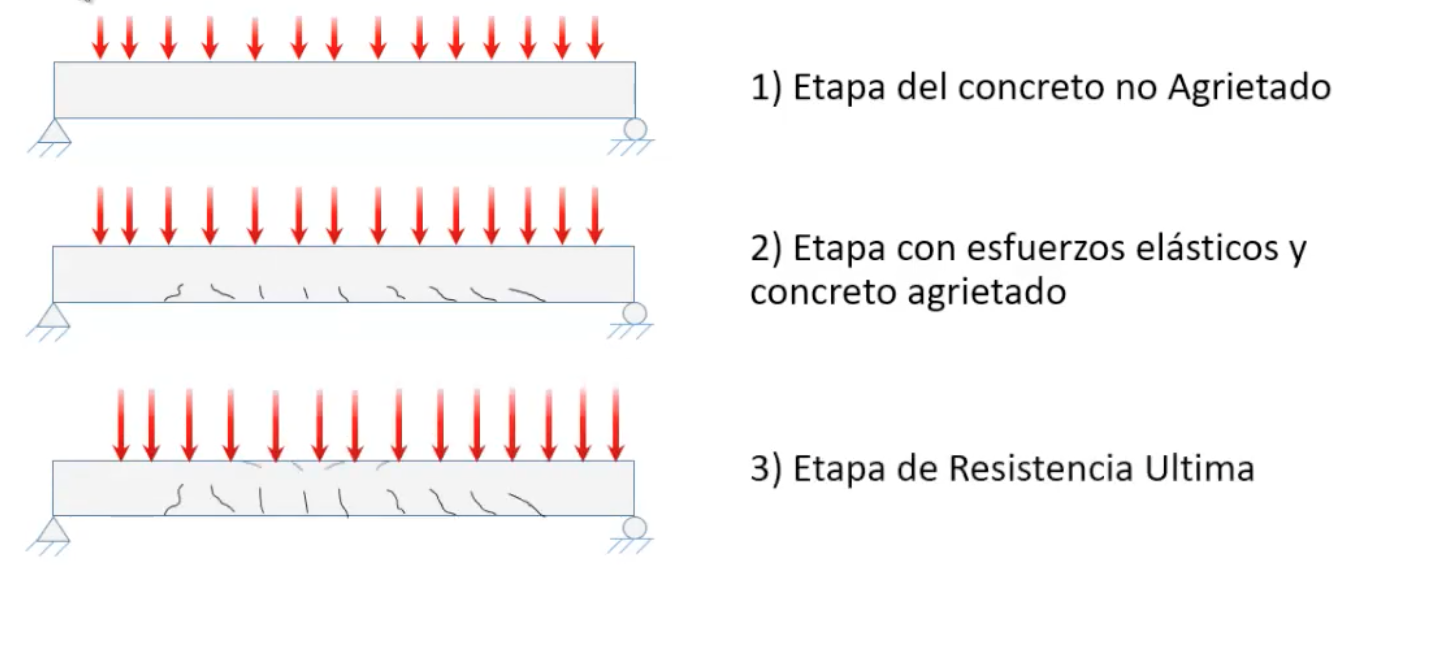
En general, en una viga la falla puede ocurrir en dos formas:
a) Una de ellas se presenta cuando el acero de refuerzo alcanza su límite elástico aparente o límite de fluencia Fy; sin que el concreto llegue aún a su fatiga de ruptura 0.85 F`c. La viga se agrietará fuertemente del lado de tensión rechazando al eje neutro hacia las fibras más comprimidas, lo que disminuye el área de compresión, aumentando las fatigas del concreto hasta presentarse finalmente la falla de la pieza. Estas vigas se llaman “Subreforzadas” y su falla ocurre más ó menos lentamente y va precedida de fuertes deflexiones y grietas que la anuncian con anticipación.
b) El segundo tipo de falla se presenta cuando el concreto alcanza su límite 0.85 F`c mientras que el acero permanece por debajo de su fatiga Fy. Este tipo de falla es súbita y prácticamente sin anuncio previo, la cual la hace muy peligrosa. Las vigas que fallan por compresión se llaman “Sobrereforzadas”.
Puede presentarse un tipo de viga cuya falla ocurra simultáneamente para ambos materiales, es decir, que el concreto alcance su fatiga límite de compresión 0.85 F’c, a la vez que el acero llega también a su límite Fy. A estas vigas se les da el nombre de “Vigas Balanceadas” y también son peligrosas por la probabilidad de la falla de compresión.
Para evitar las vigas sobre reforzadas y las balanceadas, el reglamento del ACI 318-04 limita el porcentaje de refuerzo al 75% del valor correspondiente a las secciones balanceadas. Por otra parte, también las vigas con porcentajes muy pequeños, suelen fallar súbitamente; para evitar ese riesgo el reglamento ACI 318-04 exige que el porcentaje mínimo en miembros sujetos a flexión sea de:
ρ = 14.5 / Fy , El porcentaje de la sección balanceada (Expresión 1), La expresión representa el valor del porcentaje de refuerzo en la sección balanceada de una viga.
El reglamento ACI 318-04 limita el porcentaje máximo aplicable a miembros sujetos a flexión, a 75% de ese valor por las razones ya explicadas (Expresión 2).
Una viga de concreto es rectangular, cuando su sección transversal en compresión tiene esa forma. Es simplemente armada, cuando sólo tiene refuerzo para tomar la componente de tensión del par interno.
En general, en una viga la falla puede ocurrir en dos formas:
a) Una de ellas se presenta cuando el acero de refuerzo alcanza su límite elástico aparente o límite de fluencia Fy; sin que el concreto llegue aún a su fatiga de ruptura 0.85 F`c. La viga se agrietará fuertemente del lado de tensión rechazando al eje neutro hacia las fibras más comprimidas, lo que disminuye el área de compresión, aumentando las fatigas del concreto hasta presentarse finalmente la falla de la pieza. Estas vigas se llaman “Subreforzadas” y su falla ocurre más ó menos lentamente y va precedida de fuertes deflexiones y grietas que la anuncian con anticipación.
b) El segundo tipo de falla se presenta cuando el concreto alcanza su límite 0.85 F`c mientras que el acero permanece por debajo de su fatiga Fy. Este tipo de falla es súbita y prácticamente sin anuncio previo, la cual la hace muy peligrosa. Las vigas que fallan por compresión se llaman “Sobrereforzadas”.
Puede presentarse un tipo de viga cuya falla ocurra simultáneamente para ambos materiales, es decir, que el concreto alcance su fatiga límite de compresión 0.85 F’c, a la vez que el acero llega también a su límite Fy. A estas vigas se les da el nombre de “Vigas Balanceadas” y también son peligrosas por la probabilidad de la falla de compresión.
Para evitar las vigas sobre reforzadas y las balanceadas, el reglamento del ACI 318-04 limita el porcentaje de refuerzo al 75% del valor correspondiente a las secciones balanceadas. Por otra parte, también las vigas con porcentajes muy pequeños, suelen fallar súbitamente; para evitar ese riesgo el reglamento ACI 318-04 exige que el porcentaje mínimo en miembros sujetos a flexión sea de:
ρ = 14.5 / Fy , El porcentaje de la sección balanceada (Expresión 1), La expresión representa el valor del porcentaje de refuerzo en la sección balanceada de una viga.
El reglamento ACI 318-04 limita el porcentaje máximo aplicable a miembros sujetos a flexión, a 75% de ese valor por las razones ya explicadas (Expresión 2).
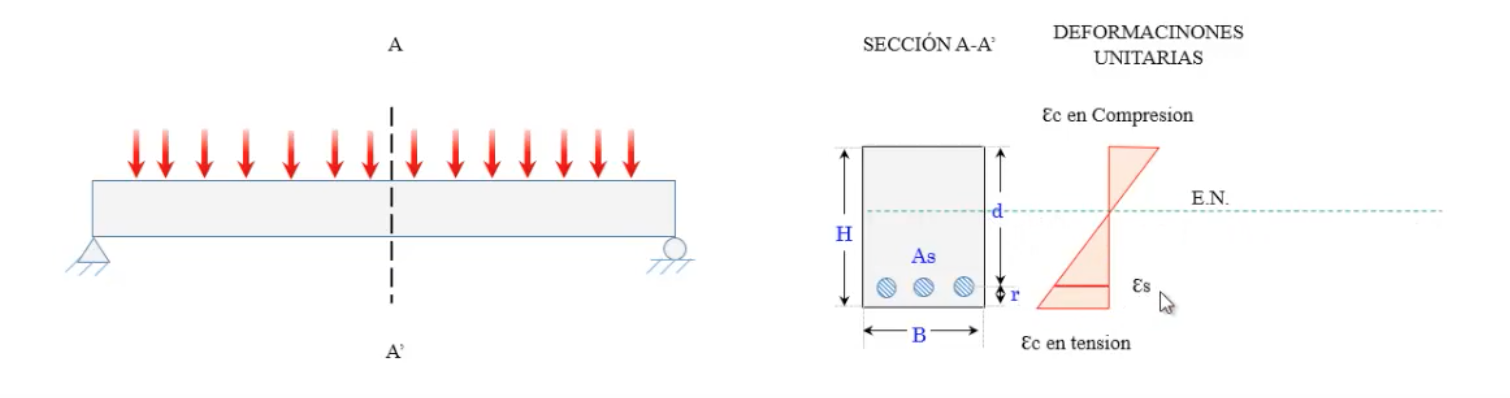
DISTRIBUCIÓN DE ESFUERZOS
|
Viga flexionada por su propio peso.
|
Bloque de esfuerzo equivalente. (Whitney 1930)
Del ACI -14 capitulo 22 tabla 22.2.2.4.3 valores para B1
Recordando:
Nota: si a > d, entonces tiene demasiado acero.
Deformaciones y esfuerzos en una viga rectangular.
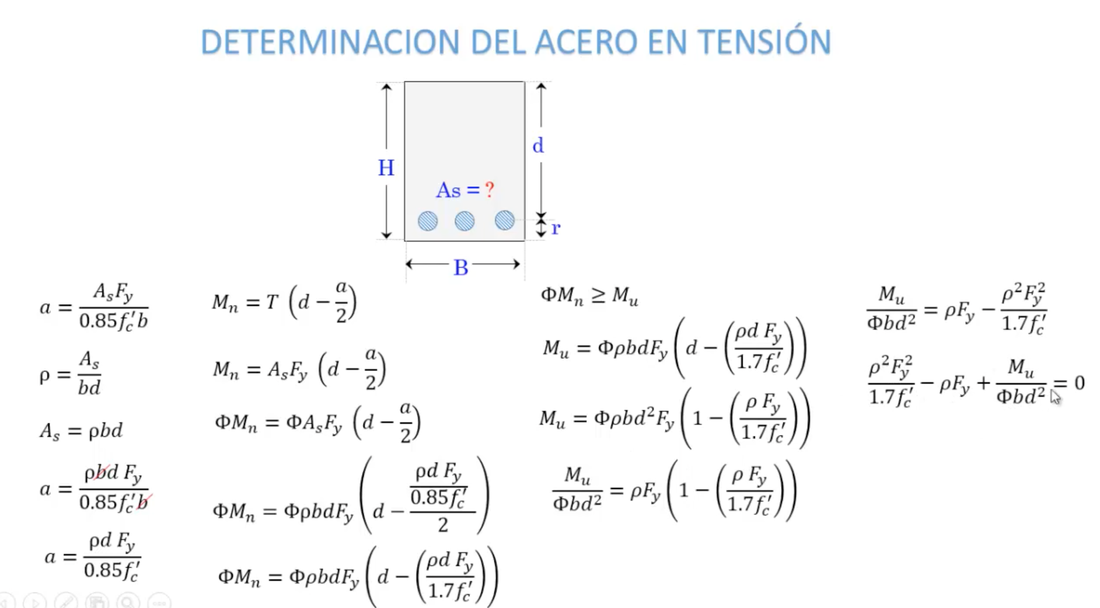
Expresiones empleadas:
Momento Último
|
Momento último, en función del acero de refuerzo
|
Ambas expresiones del momento último, el reglamento las propone afectadas de un coeficiente de seguridad que como ya se vio, para las vigas vale 0.9, por lo que quedarían finalmente:
Índice de refuerzo
En la formula anterior, únicamente se toma el signo negativo ya que si tomamos el valor positivo del radical resultaría “W” muy alto y al calcular el porcentaje de acero “ρ ” con ρ =ω F`c , resultaría mayor que el máximo Fy permisible, ρmax = 0.75ρb Así que:
Secciones Balanceadas:
Falla Frágil.
Viga Sobrereforzada o Balanceada.
Falla Dúctil.
Viga SubReforzada
Expresión 1
|
Expresión 2
|
Acero Mínimo en Vigas (ACI)
Modulo de Elasticidad del Concreto:
Ec = 14,000 * Raíz cuadrada de f'c ( Concretos premezclados, peso)
Ec = 8,000 * Raíz cuadrada de f'c ( Concretos hechos en obra , volumen)
Ec = 14,000 * Raíz cuadrada de f'c ( Concretos premezclados, peso)
Ec = 8,000 * Raíz cuadrada de f'c ( Concretos hechos en obra , volumen)
|
Convertidor de unidades :
KIPS a Kilogramos fuerza |