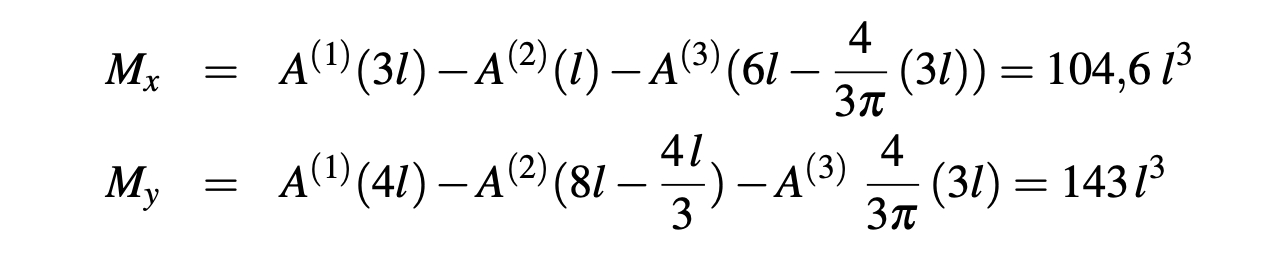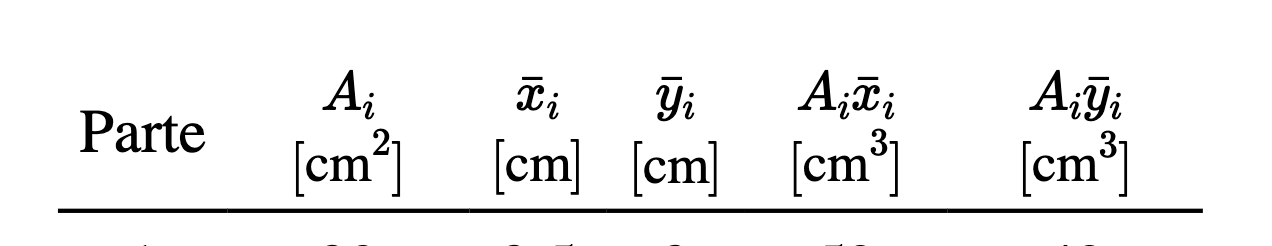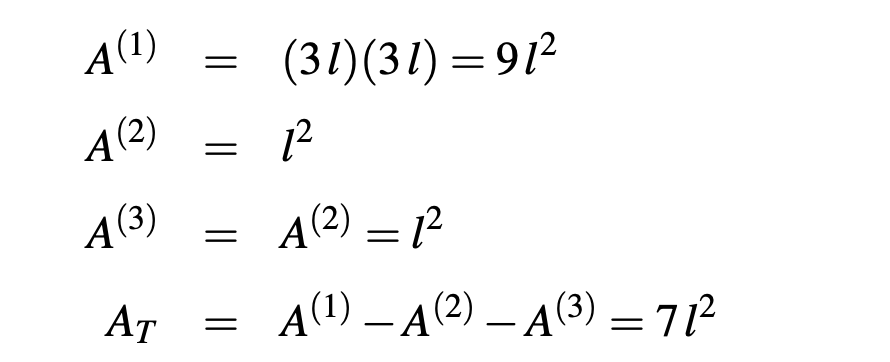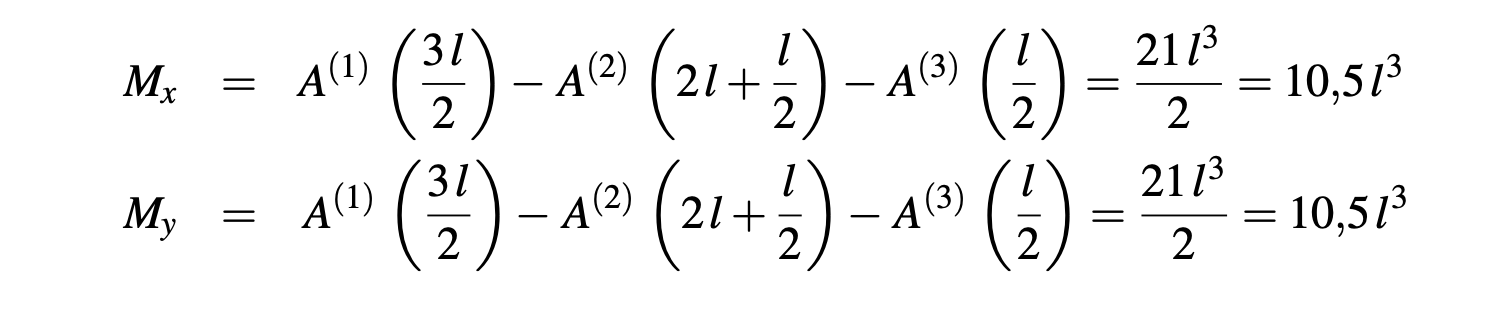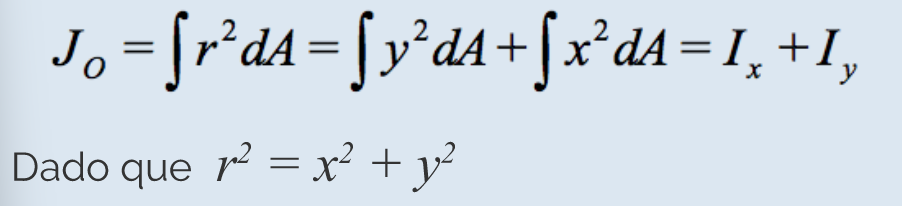Propiedades de la Sección Transversal
La importancia de la forma en el Diseño
|
Contenido:
• Definiciones.
|
Objetivos:
• Determinar centroides para áreas planas simples y para áreas planas compuestas. • Usar los teoremas de Pappus Guldinus para encontrar el área de una superficie de revolución o el volumen de un cuerpo en revolución. |
El diseño de elementos estructurales requiere el conocimiento de las cargas externas aplicadas y las reacciones internas, las resistencias de los materiales y las propiedades de la sección transversal.
Las propiedades geométricas de un elemento estructural son críticas para mantener los esfuerzos: Axiales, cortantes y de flexión dentro de los límites permitidos y regular la deflexión.
Las propiedades geométricas de un elemento estructural son críticas para mantener los esfuerzos: Axiales, cortantes y de flexión dentro de los límites permitidos y regular la deflexión.
- Por lo tanto el comportamiento de un miembro estructural está dictaminado por su material y su geometría.
- La sección transversal y la longitud del miembro estructural afectan cuánto se desvía ese miembro bajo una carga, y la sección transversal determina las tensiones que existen en el miembro bajo una carga dada.
|
|
LONDRES, 1 ago (Xinhua) -- Lu Xiaojun de China rompió hoy el récord mundial y ganó la medalla olímpica de oro en levantamiento de pesas varonil categoría de 77 kilogramos.
Lu levantó 175 kilos en el arraque y 204 kilos en el envión para un total de 379 kilogramos, con lo cual rompió su propia marca de 378 kilos.
Lu levantó 175 kilos en el arraque y 204 kilos en el envión para un total de 379 kilogramos, con lo cual rompió su propia marca de 378 kilos.
Propiedades de las áreas
Centro de Gravedad y Centroide.
El centroide es un punto que define el centro geométrico de un objeto.
El centroide coincide con el centro de masa o el centro de gravedad solo si el material del cuerpo es homogéneo (la densidad o el peso específico es constante en todo el cuerpo).
Si un objeto tiene un eje de simetría, entonces el centroide del objeto se encuentra en ese eje.
El centroide coincide con el centro de masa o el centro de gravedad solo si el material del cuerpo es homogéneo (la densidad o el peso específico es constante en todo el cuerpo).
Si un objeto tiene un eje de simetría, entonces el centroide del objeto se encuentra en ese eje.
En algunos casos, el centroide no se encuentra en el objeto
La tierra ejerce una fuerza gravitacional sobre cada una de las partículas que forman un cuerpo. Todas estas fuerzas pueden representarse mediante una única fuerza equivalente igual al peso del cuerpo y aplicarse en el centro de gravedad del cuerpo.
El centroide de una área plana representa el punto sobre el cual se distribuye uniformemente el área de la sección.
Si el área es doblemente simétrica respecto de dos ejes ortogonales, el centroide se encuentra en la intersección de esos ejes.
Si el área es simétrica con respecto a un solo eje, entonces el centroide se encuentra en algún lugar a lo largo de ese eje (será necesario calcular la otra coordenada).
Si la ubicación exacta del centroide no se puede determinar mediante inspección, se puede calcular aplicando el principio del Teorema del eje paralelo, que se mostrará más adelante.
Si el área es doblemente simétrica respecto de dos ejes ortogonales, el centroide se encuentra en la intersección de esos ejes.
Si el área es simétrica con respecto a un solo eje, entonces el centroide se encuentra en algún lugar a lo largo de ese eje (será necesario calcular la otra coordenada).
Si la ubicación exacta del centroide no se puede determinar mediante inspección, se puede calcular aplicando el principio del Teorema del eje paralelo, que se mostrará más adelante.
Diferencia entre centro de gravedad y centroide
|
Centro de Gravedad.
|
Centroide
|
Centro de Gravedad.
|
Centroide.
|
|
Distancia centroidal
La distancia centroidal ,C, es la distancia desde el centroide de una sección transversal hasta la fibra extrema. En el caso de un sólido continuo: El centro de gravedad de una sección plana se obtiene a partir de la posición de los distintos diferenciales de área del sólido, divididos por el área total del mismo. Referido a unos ejes x e y. |
|
Método analítico para obtener
centroides de áreas
centroides de áreas
Definición de Área en Matemáticas:
Es la medida de la región o superficie encerrada por de una figura geométrica.
las coordenadas de los centroides se tomaran a partir de la esquina inferior izquierda, esto nos indica que estaremos trabajando con primer cuadrante cartesiano.
En el siguiente enlace se muestran las fórmulas de área (A) y momento de inercia (I), de figuras planas.
| propiedades_de_areas_planas.pdf |
El problema surge cuando nos enfrentamos a figuras en la que no se detectan formas regulares claras, para ello utilizaremos un método denominado:
Método de piezas compuestas.
Analizaremos cómo encontrar los centroides de formas bidimensionales dividiéndolas primero en partes con propiedades conocidas y luego combinando las partes para encontrar el centroide de la forma original.
Este método funcionará cuando las propiedades geométricas de todas las subformas sean conocidas o puedan determinarse fácilmente.
Método de piezas compuestas.
Analizaremos cómo encontrar los centroides de formas bidimensionales dividiéndolas primero en partes con propiedades conocidas y luego combinando las partes para encontrar el centroide de la forma original.
Este método funcionará cuando las propiedades geométricas de todas las subformas sean conocidas o puedan determinarse fácilmente.
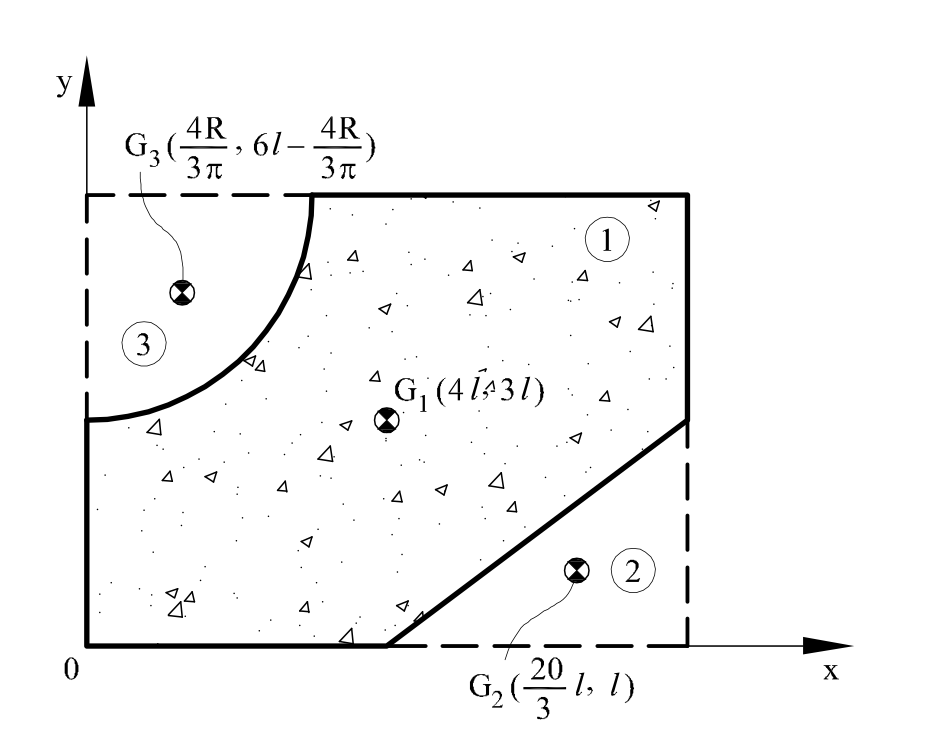
Ejemplo, encontrar el centroide la siguiente figura
Esquema de figura compleja
Procedimiento:
1) Dividir la figura compleja en figuras planas conocidas
2) Ubicar la figura dentro del primer cuadrante (para obtener distancias positivas)
3) Encontrar el área de cada una de las figuras en la cuales de dividió la figura compleja
3) Calcular la distancia del centro de gravedad de cada una de las figuras hasta el eje del primer cuadrante.
1) Dividir la figura compleja en figuras planas conocidas
2) Ubicar la figura dentro del primer cuadrante (para obtener distancias positivas)
3) Encontrar el área de cada una de las figuras en la cuales de dividió la figura compleja
3) Calcular la distancia del centro de gravedad de cada una de las figuras hasta el eje del primer cuadrante.
Se dividió la figura en 3 figuras planas conocidas
1) Rectángulo
2) Triangulo
3) Segmento Circular 1/4 de circulo.
Se localizaron la Posición de los centroides
considerados en el despiece
Cálculo del área y del centroide de la sección compuesta.
Si se analiza la geometría de la sección propuesta, se observa como ésta se puede ver cómo:
una sección rectangular (1)
a la cual se resta un triángulo (2) y
un cuarto de círculo (3)
como se muestra en la figura. De esta forma, el área de la sección compuesta, AT , resulta:
una sección rectangular (1)
a la cual se resta un triángulo (2) y
un cuarto de círculo (3)
como se muestra en la figura. De esta forma, el área de la sección compuesta, AT , resulta:
El valor de los momentos estáticos se calculan como:
Finalmente la posición del centroide, se obtiene como:
Se recomienda el siguiente procedimiento para evitar errores en las operaciones:
Registre la información que recopile en una tabla.
La tabla debe incluir una fila que contenga encabezados de columna y unidades, una fila para cada parte y una fila de resumen. La primera columna identifica la parte, por número o croquis, la segunda contiene las áreas y la tercera y cuarta contienen las coordenadas centroidales de las partes.
Registre la información que recopile en una tabla.
La tabla debe incluir una fila que contenga encabezados de columna y unidades, una fila para cada parte y una fila de resumen. La primera columna identifica la parte, por número o croquis, la segunda contiene las áreas y la tercera y cuarta contienen las coordenadas centroidales de las partes.
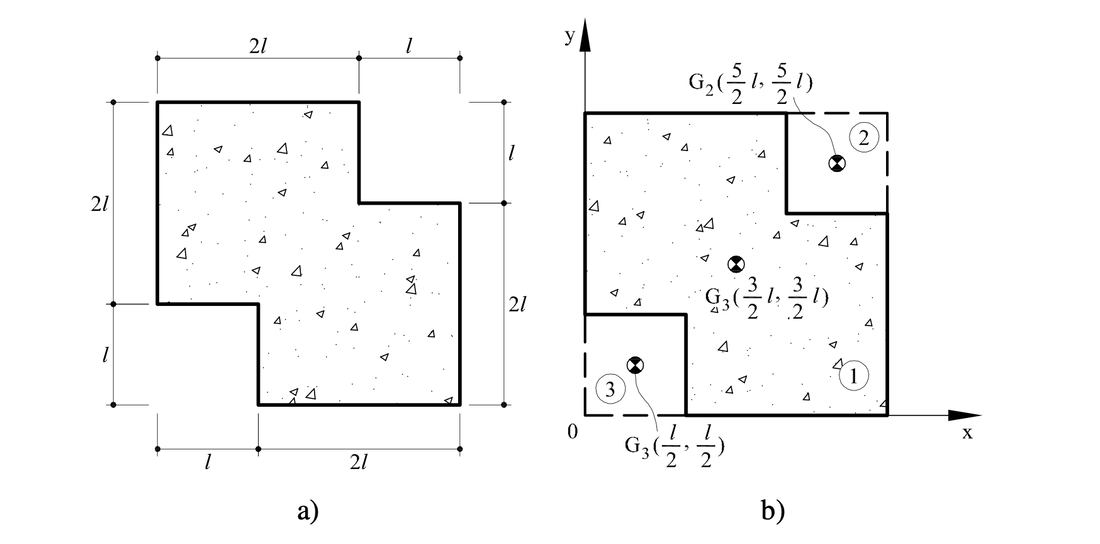
Ejemplo 2: Encontrar el centroide de la figura siguiente.
Cálculo del área y centroide la sección compuesta.
Obtención de los momentos estáticos.
Finalmente, posición del centroide de la sección compuesta.
Otras propiedades de las secciones transversales:
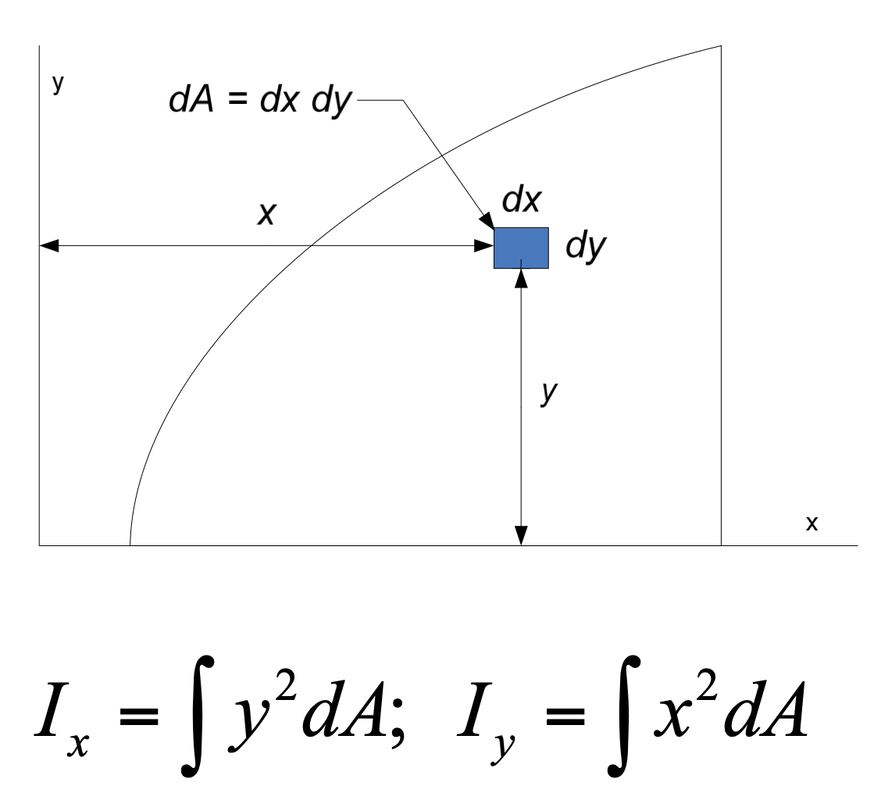
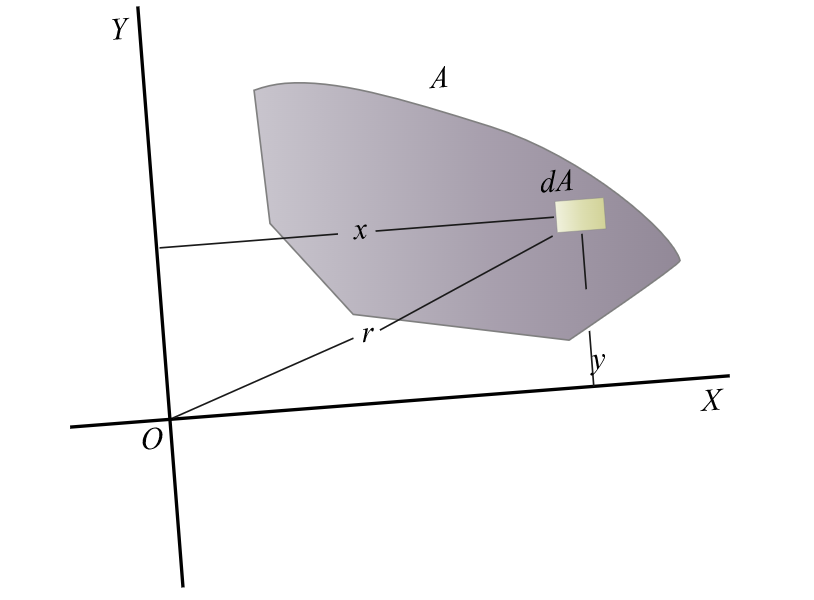
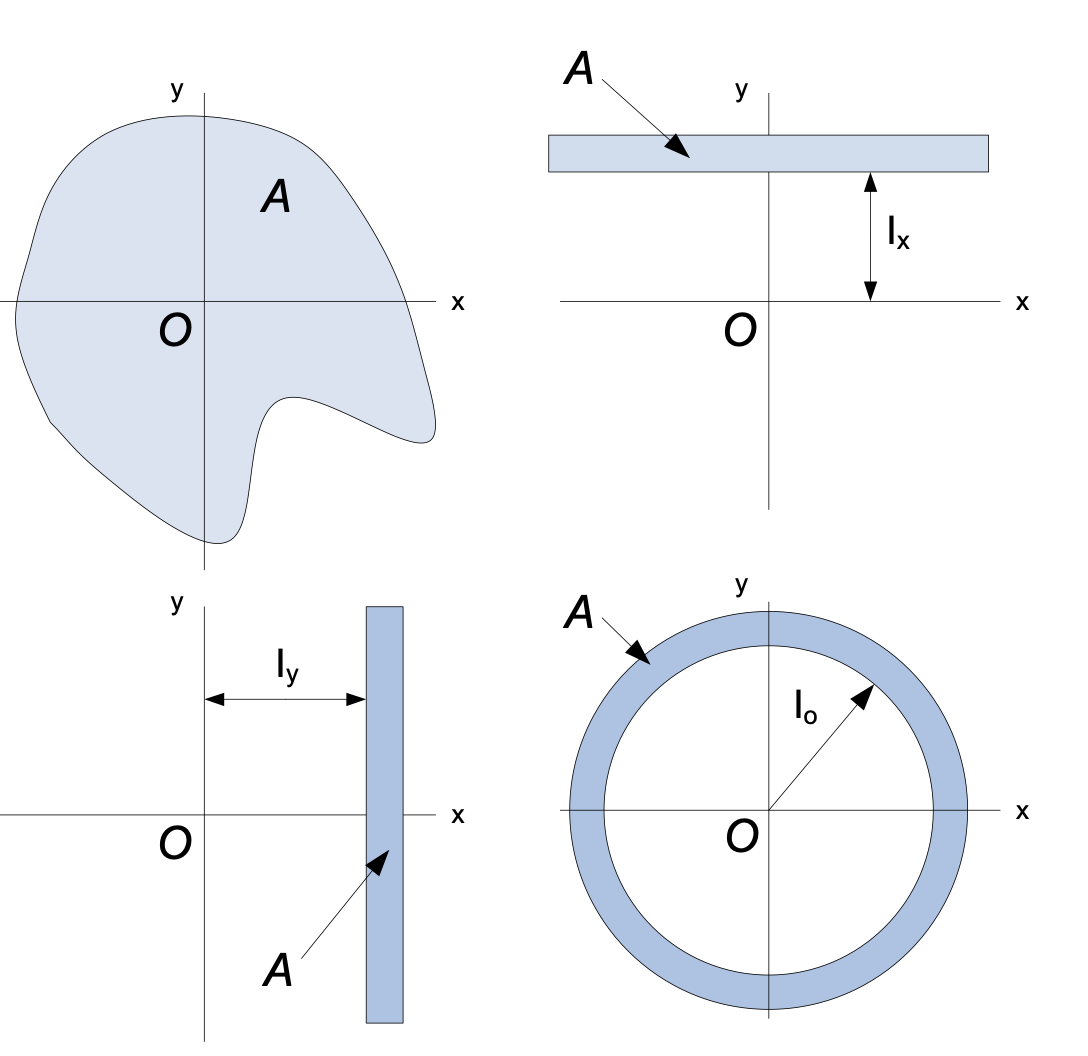
Primer momento de área (Momento de Inercia)
El centroide es proporcional a la ubicación del área asociada. Por otra parte, tenemos una medida denominada momento de inercia que no depende solamente de la ubicación del área sino de la distancia hasta un eje dado.
El momento de inercia es una propiedad geométrica de una superficie o área que representa la distancia de un área con respecto a un eje dado. Se define como la suma de los productos de todas las áreas elementales multiplicadas por el cuadrado de las distancias a un eje.
El centroide es proporcional a la ubicación del área asociada. Por otra parte, tenemos una medida denominada momento de inercia que no depende solamente de la ubicación del área sino de la distancia hasta un eje dado.
El momento de inercia es una propiedad geométrica de una superficie o área que representa la distancia de un área con respecto a un eje dado. Se define como la suma de los productos de todas las áreas elementales multiplicadas por el cuadrado de las distancias a un eje.
|
Área Momento de inercia:
El centroide es proporcional a la ubicación del área asociada. Por otra parte, tenemos una medida denominada momento de inercia que no depende solamente de la ubicación del área sino de la distancia hasta un eje dado. El momento de inercia es una propiedad geométrica de una superficie o área que representa la distancia de un área con respecto a un eje dado. Se define como la suma de los productos de todas las áreas elementales multiplicadas por el cuadrado de las distancias a un eje. |
|
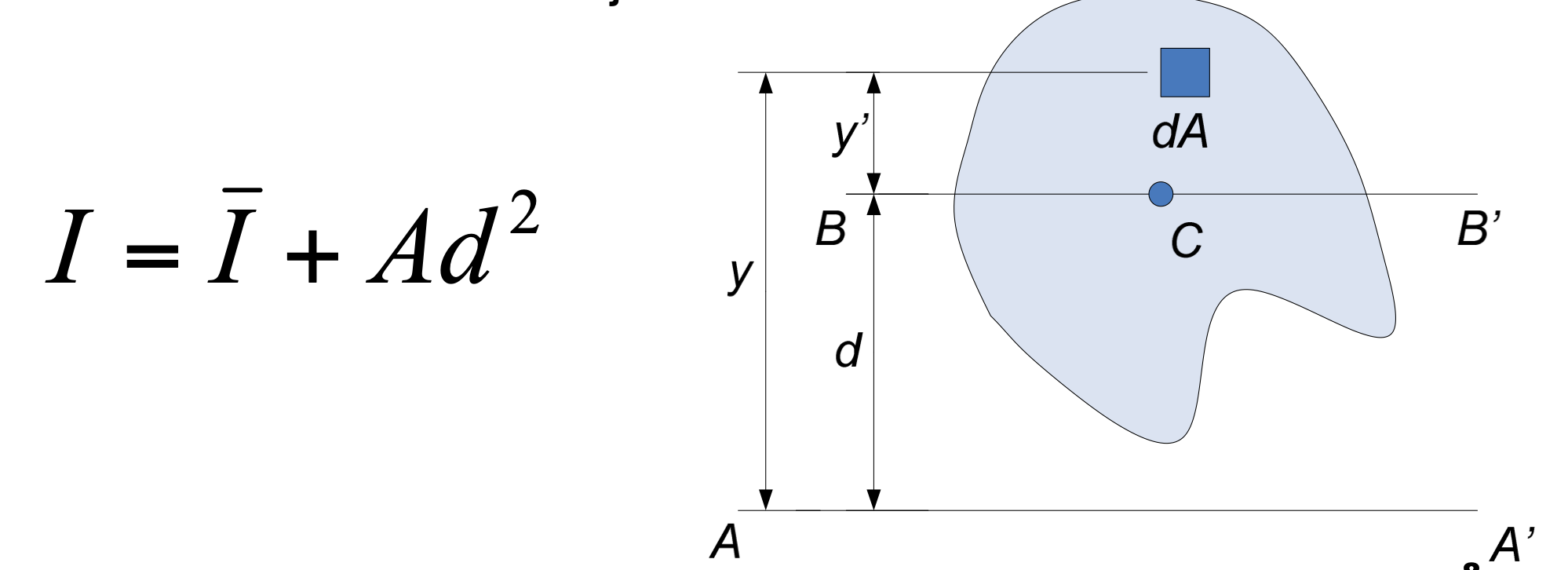
Teorema del Eje Paralelo (Steiner)Cuando se combinan superficies, los momentos de inercia de cada área requieren de la transmisión del momento de inercia al nuevo eje centroidal del área compuesta.
Esta se logra mediante el Teorema de Steiner, donde el momento de inercia con respecto a un eje dado es igual al momento de inercia con respecto al eje centroidal paralelo al eje dado más el producto del área por el cuadrado de la distancia entre los dos ejes
Esta se logra mediante el Teorema de Steiner, donde el momento de inercia con respecto a un eje dado es igual al momento de inercia con respecto al eje centroidal paralelo al eje dado más el producto del área por el cuadrado de la distancia entre los dos ejes
Momento polar de inercia
|
|
Módulo de sección
|
Radio de giro:
Si el área se concentra en una franja paralela a un eje con un A espesor diferencial, el radio de giro representa la distancia del área transformada para que tenga el mismo momento de inercia respecto al eje dado. (Beer y Johnston, 1977): |